题目内容
9.在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,CD是AB边上的高,则AD长为( )cm.| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{16}{5}$ | D. | $\frac{9}{5}$ |
分析 根据勾股定理求得AB,由三角形相似得到比例式代入数值即可求出.
解答  解:∵∠ACB=90°,CD是AB边上的高,
解:∵∠ACB=90°,CD是AB边上的高,
∴∠ACB=∠ADC=90°,
∵AC=3cm,BC=4cm,
∴AB=$\sqrt{{{AC}^{2}+BC}^{2}}$=5cm,
∵∠A=∠A,
∴△ACD∽△ABC,
∴$\frac{AC}{AB}$=$\frac{AD}{AC}$,
∴AD=$\frac{{AC}^{2}}{AB}$=$\frac{9}{5}$.
故选D.
点评 本题考查了相似三角形的判定和性质,勾股定理,证明△ACD∽△ABC是解题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
1.某初中学校现有学生500人,计划一年后男生增加5%,女生增加4%,这样总人数将增加4.5%,设该校现有男生x人,女生y人,可得方程组为( )
| A. | $\left\{\begin{array}{l}{x+y=500\\;}\\{5%x+4%y=4.5%}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=500\\;}\\{5%x+4%y=500×4.5%}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=500}\\{105%x+104%y=500+4.5%}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=500}\\{104%x+105%y=500×104.5%}\end{array}\right.$ |
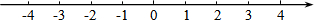 解不等式组,并把解集在数轴上表示出来.
解不等式组,并把解集在数轴上表示出来.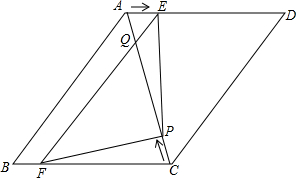 如图,在?ABCD中,AB=6cm,AD=AC=5cm,点P由C出发沿CA方向匀速运动,速度为1cm/s;同时,线段EF由AB出发沿AD方向匀速运动,速度为1cm/s,交AC于Q,连接PE、PF,若运动时间为t(s)(0<t<2.5).解答下列问题:
如图,在?ABCD中,AB=6cm,AD=AC=5cm,点P由C出发沿CA方向匀速运动,速度为1cm/s;同时,线段EF由AB出发沿AD方向匀速运动,速度为1cm/s,交AC于Q,连接PE、PF,若运动时间为t(s)(0<t<2.5).解答下列问题: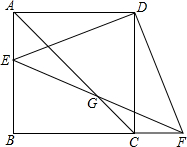 如图,在正方形ABCD中,AB=1,E为边AB上的一点(点E不与端点A、B重合),F为BC延长线上的一点,且AE=CF,联结EF交对角线AC于点G.
如图,在正方形ABCD中,AB=1,E为边AB上的一点(点E不与端点A、B重合),F为BC延长线上的一点,且AE=CF,联结EF交对角线AC于点G.
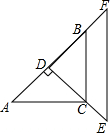 已知:有两块完全相同的含45°角的三角板,如图,将Rt△DEF的直角的顶点D放在Rt△ABC斜边AB的中点处,这时两块三角板重叠部分△DBC的面积是△ABC的面积的$\frac{1}{2}$.
已知:有两块完全相同的含45°角的三角板,如图,将Rt△DEF的直角的顶点D放在Rt△ABC斜边AB的中点处,这时两块三角板重叠部分△DBC的面积是△ABC的面积的$\frac{1}{2}$.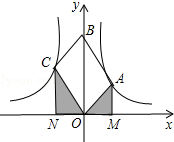 如图,OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线$y=\frac{k_1}{x}$和y=$\frac{{k}_{2}}{x}$的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①$\frac{AM}{CN}$=$\frac{|{k}_{1}|}{|{k}_{2}|}$;②阴影部分面积是$\frac{1}{2}$(k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是( )
如图,OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线$y=\frac{k_1}{x}$和y=$\frac{{k}_{2}}{x}$的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①$\frac{AM}{CN}$=$\frac{|{k}_{1}|}{|{k}_{2}|}$;②阴影部分面积是$\frac{1}{2}$(k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是( )