题目内容
3．已知两条线段的长分别为$\sqrt{2}$cm、$\sqrt{3}$cm，那么能与它们组成直角三角形的第三条线段的长是$\sqrt{5}$cm或1cm．分析 根据勾股定理的逆定理列出方程解即可，有第三边是斜边或者是直角边两种情况．
解答 解：根据勾股定理的逆定理列出方程解即可，有第三边是斜边或者是直角边两种情况．
当第三边是斜边时，第三边=$\sqrt{（\sqrt{2}）^{2}+（\sqrt{3}）^{2}}$=$\sqrt{2+3}$=$\sqrt{5}$（cm）；
当第三边是直角边时，第三边=$\sqrt{（\sqrt{3}）^{2}-（\sqrt{2}）^{2}}$=1（cm）．
综上所述，第三条线段的长是$\sqrt{5}$cm或1cm．
故答案为：$\sqrt{5}$cm或1cm．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
百年学典课时学练测系列答案
仁爱英语同步练习册系列答案
相关题目
一副三角板如图摆放，边DE∥AB，则∠1=105°．
11．
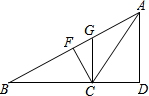如图，AD⊥BC于点D，GC⊥BC于点C，CF⊥AB于点F，下列关于高的说法中错误的是（ ）
如图，AD⊥BC于点D，GC⊥BC于点C，CF⊥AB于点F，下列关于高的说法中错误的是（ ）| A． | △ABC中，AD是BC边上的高 | B． | △GBC中，CF是BG边上的高 | ||
| C． | △ABC中，GC是BC边上的高 | D． | △GBC中，GC是BC边上的高 |
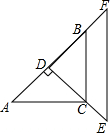已知：有两块完全相同的含45°角的三角板，如图，将Rt△DEF的直角的顶点D放在Rt△ABC斜边AB的中点处，这时两块三角板重叠部分△DBC的面积是△ABC的面积的$\frac{1}{2}$．
如图，已知梯形ABCD的四个顶点坐标分别为A（-2，1），B（-3，-2），C（3，-2），D（1，1），求梯形ABCD的面积．