题目内容
13.已知(x+y)2=1,(x-y)2=49,求:(1)xy的值;(2)x2+y2的值.分析 (1)根据(x+y)2-(x-y)2=4xy,整体代入解答;
(2)根据(x+y)2+(x-y)2=2x2+2y2,整体代入解答即可.
解答 解:(1)因为(x+y)2-(x-y)2=4xy,
可得:xy=$\frac{1}{4}$×(1-49)=-12;
(2)因为(x+y)2+(x-y)2=2x2+2y2,
可得:x2+y2=$\frac{1}{2}×$(1+49)=25.
点评 此题考查完全平方公式,关键是利用完全平方公式进行变形解答.

练习册系列答案
相关题目
2.计算-a2+3a2的结果为( )
| A. | -2a2 | B. | 2a2 | C. | 4a2 | D. | -4a2 |
1.某初中学校现有学生500人,计划一年后男生增加5%,女生增加4%,这样总人数将增加4.5%,设该校现有男生x人,女生y人,可得方程组为( )
| A. | $\left\{\begin{array}{l}{x+y=500\\;}\\{5%x+4%y=4.5%}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=500\\;}\\{5%x+4%y=500×4.5%}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x+y=500}\\{105%x+104%y=500+4.5%}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=500}\\{104%x+105%y=500×104.5%}\end{array}\right.$ |
5.计算(-a3)2的结果是( )
| A. | -a5 | B. | a5 | C. | -a6 | D. | a6 |
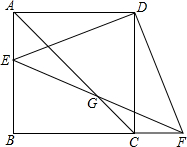 如图,在正方形ABCD中,AB=1,E为边AB上的一点(点E不与端点A、B重合),F为BC延长线上的一点,且AE=CF,联结EF交对角线AC于点G.
如图,在正方形ABCD中,AB=1,E为边AB上的一点(点E不与端点A、B重合),F为BC延长线上的一点,且AE=CF,联结EF交对角线AC于点G.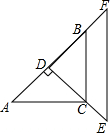 已知:有两块完全相同的含45°角的三角板,如图,将Rt△DEF的直角的顶点D放在Rt△ABC斜边AB的中点处,这时两块三角板重叠部分△DBC的面积是△ABC的面积的$\frac{1}{2}$.
已知:有两块完全相同的含45°角的三角板,如图,将Rt△DEF的直角的顶点D放在Rt△ABC斜边AB的中点处,这时两块三角板重叠部分△DBC的面积是△ABC的面积的$\frac{1}{2}$.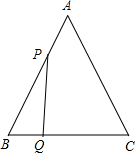 已知:如图,△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间t(s),解答下列各问题:
已知:如图,△ABC是边长为3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间t(s),解答下列各问题: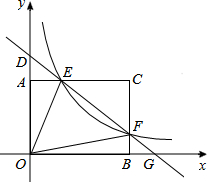 如图,矩形AOBC的顶点坐标分别为A(0,3),O(0,0),B(4,0),C(4,3),动点F在边BC上(不与B、C重合),过点F的反比例函数y=$\frac{k}{x}$的图象与边AC交于点E,直线EF分别与y轴和x轴相交于点D和G,给出下列命题:
如图,矩形AOBC的顶点坐标分别为A(0,3),O(0,0),B(4,0),C(4,3),动点F在边BC上(不与B、C重合),过点F的反比例函数y=$\frac{k}{x}$的图象与边AC交于点E,直线EF分别与y轴和x轴相交于点D和G,给出下列命题: