题目内容
 如图,在Rt△ABC中,AC=BC,AC⊥BC,AE⊥BE,AE=
如图,在Rt△ABC中,AC=BC,AC⊥BC,AE⊥BE,AE=| 1 |
| 2 |
考点:全等三角形的判定与性质,等腰三角形的判定与性质
专题:证明题
分析:延长BC,AE交于点F,易证∠CBD=∠EAD,即可证明△ACF≌△BCD,可得AF=BC,即可证明BE垂直平分AF,根据等腰三角形底边三线合一性质即可解题.
解答:证明:延长BC,AE交于点F,

∵∠ADE=∠BDC,∠EAD+∠ADE=90°,∠CBD+∠BDC=90°,
∴∠CBD=∠EAD,
∵在△ACF和△BCD中,
,
∴△ACF≌△BCD,(ASA)
∴AF=BC,
∵BC=2AF,
∴AE=EF,
∵BE⊥AF,
∴BE垂直平分AF,
∴AB=BF,
∵等腰△ABF中,E是AF中点,且BE⊥AF,
∴∠ABD=∠CBD,即BE平分∠ABC.

∵∠ADE=∠BDC,∠EAD+∠ADE=90°,∠CBD+∠BDC=90°,
∴∠CBD=∠EAD,
∵在△ACF和△BCD中,
|
∴△ACF≌△BCD,(ASA)
∴AF=BC,
∵BC=2AF,
∴AE=EF,
∵BE⊥AF,
∴BE垂直平分AF,
∴AB=BF,
∵等腰△ABF中,E是AF中点,且BE⊥AF,
∴∠ABD=∠CBD,即BE平分∠ABC.
点评:本题考查了全等三角形的判定,考擦好了全等三角形对应边相等的性质,考查了等腰三角形底边三线合一的性质,本题中求证△ACF≌△BCD是解题的关键.

练习册系列答案
相关题目
下列命题中,真命题的个数是( )
(1)等腰三角形两腰上的高相等;
(2)在空间中,垂直于同一直线的两条直线平行;
(3)两条直线被第三条直线所截,内错角相等;
(4)一个角的两边与另一个角的两边分别平行,则这两个角相等.
(1)等腰三角形两腰上的高相等;
(2)在空间中,垂直于同一直线的两条直线平行;
(3)两条直线被第三条直线所截,内错角相等;
(4)一个角的两边与另一个角的两边分别平行,则这两个角相等.
| A、1 | B、2 | C、3 | D、4 |
已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:
则方程ax2+bx+c=0的正数解x1的取值范围是( )
| x | … | -4 | -3 | -2 | -1 | 0 | … |
| y | … | 3 | -2 | -5 | -6 | -5 | … |
| A、0<x1<1 |
| B、1<x1<2 |
| C、2<x1<3 |
| D、3<x1<4 |
 用半径R=8mm,r=5mm的钢球测量口小内大的内孔的直径D,测得钢球顶点与孔口平面的距离分别为a=12.5mm,b=8.3mm(如图),计算出内孔直径D的大小(精确到0.1mm)
用半径R=8mm,r=5mm的钢球测量口小内大的内孔的直径D,测得钢球顶点与孔口平面的距离分别为a=12.5mm,b=8.3mm(如图),计算出内孔直径D的大小(精确到0.1mm) 如图,壁虎在一个圆柱形油罐的下底边沿A处,它发现在B处有一只苍蝇,壁虎决定尽快捉到这只苍蝇,获得一顿美餐,请问壁虎从A处到B处的最短路线是什么?
如图,壁虎在一个圆柱形油罐的下底边沿A处,它发现在B处有一只苍蝇,壁虎决定尽快捉到这只苍蝇,获得一顿美餐,请问壁虎从A处到B处的最短路线是什么?
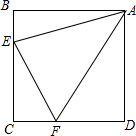 如图,四边形ABCD是边长为1的正方形,△ECF周长为2,求∠EAF的大小.
如图,四边形ABCD是边长为1的正方形,△ECF周长为2,求∠EAF的大小. 如图,在四边形ABCD中,AB=DC,∠ABC=∠DCB,点E、F分别在AB、BC上,且BE=2AE,CF=2DF.求证:∠BEC=∠CFB.
如图,在四边形ABCD中,AB=DC,∠ABC=∠DCB,点E、F分别在AB、BC上,且BE=2AE,CF=2DF.求证:∠BEC=∠CFB.