题目内容
16.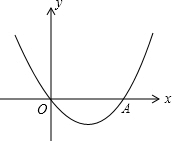 如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).
如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).(1)求此抛物线的解析式;
(2)求此抛物线顶点坐标及对称轴;
(3)若抛物线上有一点B,且S△OAB=1,求点B的坐标.
分析 (1)利用交点式求抛物线解析式;
(2)把(1)中解析式配成顶点式即可得到抛物线顶点坐标及对称轴;
(3)设B(t,t2-2t),根据三角形面积公式得到$\frac{1}{2}$×2×|t2-2t|=1,则t2-2t=1或t2-2t=-1,然后分别解两个方程求出t,从而可得到B点坐标.
解答 解:(1)抛物线解析式为y=x(x-2),即y=x2-2x;
(2)因为y=x2-2x=(x-1)2-1,
所以抛物线的顶点坐标为(1,-1),对称轴为直线x=1;
(3)设B(t,t2-2t),
因为S△OAB=1,
所以$\frac{1}{2}$×2×|t2-2t|=1,
所以t2-2t=1或t2-2t=-1,
解方程t2-2t=1得t1=1+$\sqrt{2}$,t2=1-$\sqrt{2}$,则B点坐标为(1+$\sqrt{2}$,1)或(1-$\sqrt{2}$,1);
解方程t2-2t=-1得t1=t2=1,则B点坐标为(1,-1),
所以B点坐标为(1+$\sqrt{2}$,1)或(1-$\sqrt{2}$,1)或(1,-1).
点评 本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$),对称轴直线x=-$\frac{b}{2a}$.

练习册系列答案
相关题目
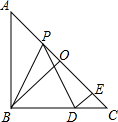 如图,在等腰直角△ABC中,O是斜边AC的中点,P是斜边AC上的一个动点,D为BC上的一点,且PB=PD,DE⊥AC,垂足为E.
如图,在等腰直角△ABC中,O是斜边AC的中点,P是斜边AC上的一个动点,D为BC上的一点,且PB=PD,DE⊥AC,垂足为E. 已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于E,交BC边于F,分别连接AF和CE,AE=10.
已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于E,交BC边于F,分别连接AF和CE,AE=10.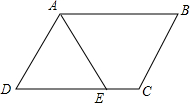 如图,在?ABCD中,AB>BC,AE平分∠BAD交CD于点E,如果?ABCD的周长为20,EC=2,求AB、BC的长.
如图,在?ABCD中,AB>BC,AE平分∠BAD交CD于点E,如果?ABCD的周长为20,EC=2,求AB、BC的长.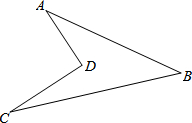 如图所示的一块土地,∠ADC=90°,AD=3m,CD=4m,AB=12m,BC=13m,求这块土地的面积.
如图所示的一块土地,∠ADC=90°,AD=3m,CD=4m,AB=12m,BC=13m,求这块土地的面积.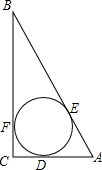 如图,⊙O为Rt△ABC的内切圆,⊙O的半径r=1,∠B=30°,
如图,⊙O为Rt△ABC的内切圆,⊙O的半径r=1,∠B=30°,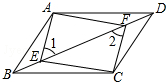 如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,BE=DF.
如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,BE=DF.