题目内容
7. 已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于E,交BC边于F,分别连接AF和CE,AE=10.
已知:如图所示的一张矩形纸片ABCD(AD>AB),将纸片折叠一次,使点A与C重合,再展开,折痕EF交AD边于E,交BC边于F,分别连接AF和CE,AE=10.(1)在线段AC上是(填“是”或“否”)存在一点P,使得2AE•CE=AC•AP;
(2)若存在,请在下图作出点P,说明点P的位置,若不存在,请说明理由:
分析 过点E作EP⊥AD交AC于P,点P就是所求的点,只要证明△AOE∽△AEP,即可求解.
解答 解:(1)是.
故答案为是.
(2)过点E作EP⊥AD交AC于P,点P就是所求的点.
理由:∵ △AEF是由△EFC翻折得到,
△AEF是由△EFC翻折得到,
∴AO=OC,AC⊥EF,EA=EC,
∴∠AOE=∠EP=90°,
∵○EAO=∠EAP,
∴△AOE∽△AEP,
∴$\frac{AO}{AE}=\frac{AE}{AP}$,
∴AE2=AO•AP,
∴2AE•EC=2AO•AP=AC•AP.
点评 本题考查翻折变换、相似三角形的判定和性质,解决问题的关键是添加辅助线构造相似三角形,属于中考常考题型.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目

 抛物线y=x2+bx+c与x轴分别交于点A(-1,0)和点B,与y轴的交点C坐标为(0,-3).
抛物线y=x2+bx+c与x轴分别交于点A(-1,0)和点B,与y轴的交点C坐标为(0,-3).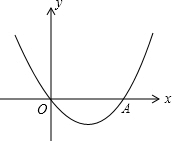 如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).
如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0). 如图,在平行四边形ABCD中,M、N分别是BC、DC的中点,AM=4,AN=3,且∠MAN=60°,则AB的长是$\frac{14}{3}$.
如图,在平行四边形ABCD中,M、N分别是BC、DC的中点,AM=4,AN=3,且∠MAN=60°,则AB的长是$\frac{14}{3}$.