题目内容
6.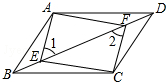 如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,BE=DF.
如图,四边形ABCD是平行四边形,E、F是对角线BD上的点,BE=DF.(1)求证:∠AEB=∠CFD;
(2)求证:AF∥CE.
分析 (1)由SAS证明△ABE≌△CDF,得出对应角相等即可;
(2)由全等三角形的对应边相等得出AE=CF,同理AF=CE,证出四边形AECF是平行四边形,即可得出结论.
解答 证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,AD∥BC,AD=BC,
∴∠ABE=∠CDF,
在△ABE和△CDF中,$\left\{\begin{array}{l}{AB=CD}&{\;}\\{∠ABE=∠CDF}&{\;}\\{BE=DF}&{\;}\end{array}\right.$,
∴△ABE≌△CDF(SAS),
∴∠AEB=∠CFD;
(2)证明:由(1)得:△ABE≌△CDF,
∴AE=CF,
同理:AF=CE,
∴四边形AECF是平行四边形,
∴AF∥CE.
点评 本题主要考查了平行四边形的判定与性质、全等三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
14. 如图,已知∠1=∠2=∠3=∠4,则图形中所有平行的是( )
如图,已知∠1=∠2=∠3=∠4,则图形中所有平行的是( )
 如图,已知∠1=∠2=∠3=∠4,则图形中所有平行的是( )
如图,已知∠1=∠2=∠3=∠4,则图形中所有平行的是( )| A. | AB∥CD∥EF | B. | CD∥EF | C. | AB∥EF | D. | AB∥CD∥EF,BC∥DE |
11.已知m是$\sqrt{5}$的小数部分,则$\sqrt{{m}^{2}+\frac{1}{{m}^{2}}-2}$的值( )
| A. | $\frac{4}{5}\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | -4 | D. | 4 |
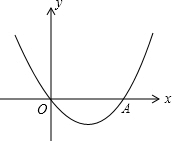 如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).
如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0). 如图,在平行四边形ABCD中,M、N分别是BC、DC的中点,AM=4,AN=3,且∠MAN=60°,则AB的长是$\frac{14}{3}$.
如图,在平行四边形ABCD中,M、N分别是BC、DC的中点,AM=4,AN=3,且∠MAN=60°,则AB的长是$\frac{14}{3}$. 如图,小俊在A处利用高为1.8米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)(参考数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.732)
如图,小俊在A处利用高为1.8米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)(参考数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.732)