题目内容
6.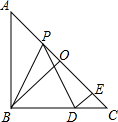 如图,在等腰直角△ABC中,O是斜边AC的中点,P是斜边AC上的一个动点,D为BC上的一点,且PB=PD,DE⊥AC,垂足为E.
如图,在等腰直角△ABC中,O是斜边AC的中点,P是斜边AC上的一个动点,D为BC上的一点,且PB=PD,DE⊥AC,垂足为E.(1)试论证PE与BO的位置关系和大小关系.
(2)设AC=2a,AP=x,四边形PBDE的面积为y,试写出y与x之间的函数关系式,并写出自变量x的取值范围.
分析 (1)利用等腰直角三角形的性质得出OB⊥AC,即可得出PE与BO的位置关系,再利用全等三角形的判定得出△POB≌△DEP(AAS),得出PE与BO的大小关系.
(2)利用S四边形PBDE=S△ABC-S△APB-S△DEC,分别求出各图形面积,得出y与x之间的函数关系即可.
解答 (1)证明:∵O是等腰直角三角形ABC斜边AC的中点,
∴OB⊥AC;∠OBC=$\frac{1}{2}$∠ABC=45°,
又∵DE⊥AC,
∴∠BOP=∠PED=90°,
∵AB=BC,∠ABC=90°,
∴∠C=∠A=45°,
∵∠PDB=∠C+∠DPE,
∴∠PDB=45°+∠DPE,
∵PB=PD,
∴∠PBD=∠PDB,
∴∠PBO+45°=45°+∠DPE,
∴∠PBO=∠DPE,
在△POB和△DEP中,
$\left\{\begin{array}{l}{∠POB=∠PED}\\{∠OBP=∠EPD}\\{PB=PD}\end{array}\right.$,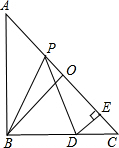
∴△POB≌△DEP(AAS),
∴PE=BO;
故PE与BO的位置关系是PE⊥BO,大小关系是:PE=BO.
(2)解:∵O是等腰直角三角形ABC斜边AC的中点
∴OB=$\frac{1}{2}$AC,OB⊥AC,
∵AC=2a,
∴PE=OB=a,
∵AP=x,
∴CE=2a-a-x=a-x,
∴S△APB=$\frac{1}{2}$x•a=$\frac{1}{2}$ax,
∵DE⊥AC,∠C=45°,DE=CE=a-x,
∴S△DEC=$\frac{1}{2}$(a-x)2,
∴S四边形PBDE=S△ABC-S△APB-S△DEC,
∴y=$\frac{1}{2}$×2a×a-$\frac{1}{2}$ax-$\frac{1}{2}$(a-x)2,
∴y=-$\frac{1}{2}$x2+$\frac{1}{2}$ax+$\frac{1}{2}$a2.
点评 此题主要考查了全等三角形的判定与性质、等腰直角三角形的性质,寻找全等三角形是解题的关键,学会用分割法求四边形面积,属于中考常考题型.

| 参加班级 | A | B | C | D |
| 得分情况 | 14 | 18 | 10 | 6 |
(2)若A班在所有的比赛中总得分为14分,则该班胜了几场?
(3)假设比赛结束后,E班得分比F,C两班得分之和的2倍还多2分,且E班获胜场数超过F,G两班获胜场数之和,请求出E班胜了几场?
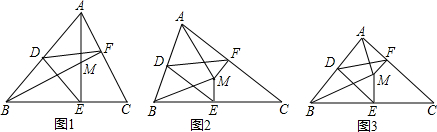
 如图,在边长为12$\sqrt{2}$的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,CF⊥EG交EG于H,交AD于F点,连接CE,BH.若BH=16,则FG=10$\sqrt{2}$.
如图,在边长为12$\sqrt{2}$的正方形ABCD中,E是AB边上一点,G是AD延长线上一点,BE=DG,连接EG,CF⊥EG交EG于H,交AD于F点,连接CE,BH.若BH=16,则FG=10$\sqrt{2}$.
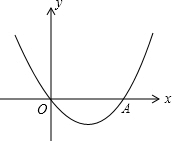 如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).
如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).