题目内容
4.计算(1)$-{2^2}+{({-\frac{1}{2}})^{-1}}+{(3-π)^0}$
(2)(-a)2•a4÷a3
(3)(2x-1)(x-3)
(4)(3x-2y)2(3x+2y)2
(5)(x-2y+4)(x-2y-4)
分析 (1)根据有理数的乘方法则、负整数指数幂的定义和零指数幂的定义计算,再合并即可;
(2)根据同底数幂的乘除法法则计算即可;
(3)根据多项式与多项式相乘的法则计算,再合并即可;
(4)先运用平方差公式计算,再运用完全平方公式计算即可;
(5)先运用平方差公式计算,再运用完全平方公式计算即可.
解答 解:(1)$-{2^2}+{({-\frac{1}{2}})^{-1}}+{(3-π)^0}$
=-4-2+1
=-5;
(2)(-a)2•a4÷a3
=a2•a4÷a3
=a3;
(3)(2x-1)(x-3)
=2x2-6x-x+3
=2x2-7x+3;
(4)(3x-2y)2(3x+2y)2
=[(3x-2y)(3x+2y)]2
=(9x2-4y2)2
=81x4-72x2y2+16y4
(5)(x-2y+4)(x-2y-4)
=(x-2y)2-42
=x2-4xy+4y2-16
点评 本题考查了整式的混合运算、有理数的乘方法则、负整数指数幂的定义和零指数幂的定义以及乘法公式;熟记负整数指数幂的定义和零指数幂的定义以及乘法公式是解决问题的关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
14. 如图,已知∠1=∠2=∠3=∠4,则图形中所有平行的是( )
如图,已知∠1=∠2=∠3=∠4,则图形中所有平行的是( )
 如图,已知∠1=∠2=∠3=∠4,则图形中所有平行的是( )
如图,已知∠1=∠2=∠3=∠4,则图形中所有平行的是( )| A. | AB∥CD∥EF | B. | CD∥EF | C. | AB∥EF | D. | AB∥CD∥EF,BC∥DE |
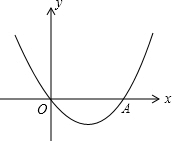 如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).
如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).