题目内容
5.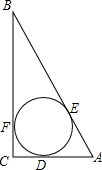 如图,⊙O为Rt△ABC的内切圆,⊙O的半径r=1,∠B=30°,
如图,⊙O为Rt△ABC的内切圆,⊙O的半径r=1,∠B=30°,(1)劣弧DE的长.
(2)证明:AD=AE.
(3)求:劣弧DE、切线AD、AE所围成的面积S.
分析 (1)根据切线的性质得出OD⊥AC,OE⊥AB,根据四边形内角和求得∠DOE=120°,代入公式求得即可;
(2)证得RT△AOD≌RT△AOE即可得到结论;
(3)根据S=S四边形ADOE-S扇形ODE求得即可.
解答 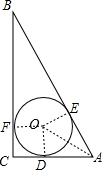 解:(1)连接OD、OE,则OD⊥A,COE⊥AB
解:(1)连接OD、OE,则OD⊥A,COE⊥AB
∵∠B=30°∠C=90°
∴∠A=60°
∴∠DOE=120°
劣弧DE的长=$\frac{120×1•π}{180}$=$\frac{2π}{3}$;
(2)连接OA,
在RT△AOD和RT△AOE中
$\left\{\begin{array}{l}{OD=OE}\\{OA=OA}\end{array}\right.$
∴RT△AOD≌RT△AOE(HL),
∴AD=AE
(3)∵RT△AOD≌RT△AOE,
∴∠OAB=∠OAC=$\frac{1}{2}$∠BAC=30°,
∴AE=$\sqrt{3}$OE=$\sqrt{3}$,
∴四边形ADOE的面积=2×$\frac{1}{2}$AE•OE=$\sqrt{3}$,
∵S扇形ODE=$\frac{120π×{1}^{2}}{360}$=$\frac{1}{3}$π
∴S=S四边形ADOE-S扇形ODE=$\sqrt{3}$-$\frac{π}{3}$.
点评 本题考查了内切圆的性质,弧长和扇形的面积,三角形求得的判定和性质以及四边形的内角和等,熟练掌握性质定理是解题的关键

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
20.市一中准备组织学生及学生家长到武汉大学参观体验,为了便于管理,所有人员到武汉必须乘坐在同一列动车上;根据报名人数,若都买一等座单程火车票需2556元,若都买二等座单程火车票且花钱最少,则需1530元;已知学生家长与教师的人数之比为2:1,安陆到武汉的动车票价格(动车学生票只有二等座可以打6折)如下表所示:
(1)参加参观体验的老师、家长与学生各有多少人?
(2)由于各种原因,二等座火车票单程只能买x张(x小于参加参观体验的人数),其余的须买一等座火车票,在保证每位参与人员都有座位坐的前提下,请你设计最经济的购票方案,并写出购买火车票的总费用(单程)y与x之间的函数关系式.
(3)请你做一个预算,按第(2)小题中的购票方案,购买单程火车票的总费用至少是多少钱?最多是多少钱?
| 运行区间 | 票价 | ||
| 上车站 | 下车站 | 一等座 | 二等座 |
| 安陆 | 武汉 | 36(元) | 30(元) |
(2)由于各种原因,二等座火车票单程只能买x张(x小于参加参观体验的人数),其余的须买一等座火车票,在保证每位参与人员都有座位坐的前提下,请你设计最经济的购票方案,并写出购买火车票的总费用(单程)y与x之间的函数关系式.
(3)请你做一个预算,按第(2)小题中的购票方案,购买单程火车票的总费用至少是多少钱?最多是多少钱?
14. 如图,已知∠1=∠2=∠3=∠4,则图形中所有平行的是( )
如图,已知∠1=∠2=∠3=∠4,则图形中所有平行的是( )
 如图,已知∠1=∠2=∠3=∠4,则图形中所有平行的是( )
如图,已知∠1=∠2=∠3=∠4,则图形中所有平行的是( )| A. | AB∥CD∥EF | B. | CD∥EF | C. | AB∥EF | D. | AB∥CD∥EF,BC∥DE |
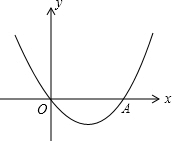 如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0).
如图,抛物线y=x2+bx+c经过坐标原点,并与x轴交于点A(2,0). 如图,在平行四边形ABCD中,M、N分别是BC、DC的中点,AM=4,AN=3,且∠MAN=60°,则AB的长是$\frac{14}{3}$.
如图,在平行四边形ABCD中,M、N分别是BC、DC的中点,AM=4,AN=3,且∠MAN=60°,则AB的长是$\frac{14}{3}$. 如图,小俊在A处利用高为1.8米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)(参考数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.732)
如图,小俊在A处利用高为1.8米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)(参考数据:$\sqrt{2}$=1.414,$\sqrt{3}$=1.732)