题目内容
13. 如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=$\sqrt{3}$,BC=1.连接BF,分别交AC、DC、DE与点P、Q、R.有下列结论①△BFG∽△ABC、②BQ=FQ、③AP=2PC、④EF平分∠BFG,你认为不正确的是④.
如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=$\sqrt{3}$,BC=1.连接BF,分别交AC、DC、DE与点P、Q、R.有下列结论①△BFG∽△ABC、②BQ=FQ、③AP=2PC、④EF平分∠BFG,你认为不正确的是④.
分析 根据△ABC、△DCE、△FEG是三个全等的等腰三角形,即可得到AB∥CD∥EF,AC∥DE∥FG,根据平行线等分线段定理即可判断.
解答 解:∵△BFG和△FEG有一个公用角∠G,
BG=3,FG=$\sqrt{3}$,EG=1,
FG:EG=BG:FG=$\sqrt{3}$,
∴△BFG∽△FEG,
故①是正确的.
∵CD∥EF,BC=CE,
∴BQ=FQ,
故②正确;
△BPC∽△BFG,
PC:FG=BC:BG,
PC=$\frac{FG}{3}$=$\frac{AC}{3}$,
∴AP=2PC,
故③正确;
故①②③正确.
故答案为:④.
点评 本题主要考查了平行线分线段定理,以及三角形相似的判定,正确理解AB∥CD∥EF,AC∥DE∥FG是解题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
2.下列说法正确的是( )
| A. | 为了了解全国中学生每天体育锻炼的时间,应采用普查的方式 | |||||||||||||
| B. | 甲组数据的方差${S_甲}^2$=0.03,乙组数据的方差是${S_乙}^2$=0.2,则乙组数据比甲组数据稳定 | |||||||||||||
| C. | 广州市明天一定会下雨 | |||||||||||||
| D. | 某班学生数学成绩统计如下,则该班学生数学成绩的众数和中位数分别是80分,80分
|
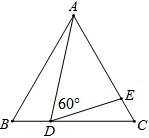 已知:如图,△ABC是等边三角形,点D、E分别在边BC、AC上,∠ADE=60°.
已知:如图,△ABC是等边三角形,点D、E分别在边BC、AC上,∠ADE=60°.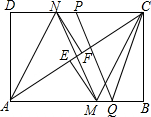 如图,在矩形ABCD中,把∠B、∠D分别翻折,使点B、D分别落在对角线BC上的点E、F处,折痕分别为CM、AN.连接MF、NE. P、Q是矩形的边CD、AB上的两点,连结PQ、CQ、MN.若PQ=CQ,PQ∥MN,且AB=4,BC=3,则PC的长度是2.
如图,在矩形ABCD中,把∠B、∠D分别翻折,使点B、D分别落在对角线BC上的点E、F处,折痕分别为CM、AN.连接MF、NE. P、Q是矩形的边CD、AB上的两点,连结PQ、CQ、MN.若PQ=CQ,PQ∥MN,且AB=4,BC=3,则PC的长度是2.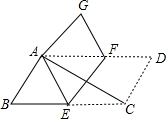 如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处,
如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处,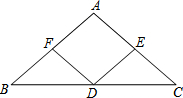 已知:如图,D是△ABC的边BC的中点,DE⊥AC、DF⊥AB,垂足分别是E、F,且BF=CE,
已知:如图,D是△ABC的边BC的中点,DE⊥AC、DF⊥AB,垂足分别是E、F,且BF=CE,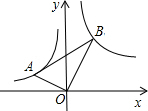 如图,在Rt△ABO中,∠AOB=90°,且OB=2AO,点A在反比例函数y=$-\frac{2}{x}$的图象上,点B比在反比例函数y=$\frac{m}{x}$的图象上,则m的值为( )
如图,在Rt△ABO中,∠AOB=90°,且OB=2AO,点A在反比例函数y=$-\frac{2}{x}$的图象上,点B比在反比例函数y=$\frac{m}{x}$的图象上,则m的值为( )