题目内容
4.已知二次函数y=ax2-4a+4(a<0)(1)若a=-1写出抛物线顶点坐标,抛物线与x轴交点坐标.
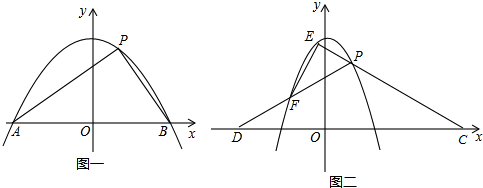
(2)如图(一)抛物线上有一点P(2,4)若抛物线与x轴交于A,B,且∠APB=90°.求a的值.
(3)如图(二)若直线y=2x+b与抛物线相交于E,F两点,过(2)中P点作直线PE,PF,与x轴交于C,D.当PC=PD时,求a的值.
分析 (1)将a=-1代入抛物线可得抛物线解析式,再根据抛物线解析式可得抛物线顶点坐标,令y=0,得到方程-x2+8=0,解方程得到抛物线与x轴交点坐标;
(2)令y=0,得ax2-4a+4=0,解方程得到x的值,从而得到A(-$\sqrt{\frac{4a-4}{a}}$,0),B($\sqrt{\frac{4a-4}{a}}$,0),OB=$\sqrt{\frac{4a-4}{a}}$,根据勾股定理可得PO=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$
,由于∠APB=90°,OA=OB,可得OB=PO,得到关于a的方程,解方程即可求解;
(3)设点E、F的坐标分别为F(x1,ax12-4a+4)、E(x2,ax22-4a+4).如图,过点E作EG∥y轴,过点P作PG∥x轴,EG、PG相交于点G,过点FH∥x轴,过点P作PH∥y轴,FH、PH相交于点H.通过相似三角形Rt△PGE∽Rt△FHP的对应边成比例得到$\frac{EG}{PG}$=$\frac{PH}{FH}$,即$\frac{2-{x}_{2}}{{ax}_{2}^{2}-4a}$=$\frac{2-{x}_{1}}{-({ax}_{1}^{2}-4a)}$,则x1+x2=-4,解方程即可求得a的值.
解答 解:(1)∵a=-1,
∴二次函数y=-x2+8.
∴二次函数的顶点坐标为:(0,8)
令y=0,-x2+8=0
解得x1=2$\sqrt{2}$,x2=-2$\sqrt{2}$,
∴A(-2$\sqrt{2}$,0),B(2$\sqrt{2}$,0)
(2)令y=0,得ax2-4a+4=0,
解得x=±$\sqrt{\frac{4a-4}{a}}$
∴A(-$\sqrt{\frac{4a-4}{a}}$,0),B($\sqrt{\frac{4a-4}{a}}$,0)
∴OB=$\sqrt{\frac{4a-4}{a}}$
∵P(2,4),
∴PO=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$
∵∠APB=90°,OA=OB,
∴OB=PO,
∴2$\sqrt{5}$=$\sqrt{\frac{4a-4}{a}}$
解得a=-$\frac{1}{4}$.
(3)设点F、E的坐标分别为F(x1,ax12-4a+4)、E(x2,ax22-4a+4).
又∵点F、E在直线y=2x+b上,
∴a(x1+x2)=2.
如图二,过点E作EG∥y轴,过点P作PG∥x轴,EG、PG相交于点G,过点FH∥x轴,过点P作PH∥y轴,FH、PH相交于点H.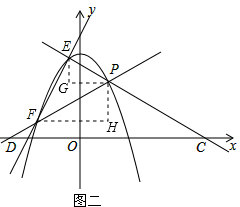
∵PD=PC,
∴∠PDC=∠PCD.
∵FH∥x轴,
∴∠PFH=∠PDC.
同理,∠EPG=∠PCD,
∴∠FHP=∠PGE,
∴Rt△PGE∽Rt△FHP,
∴$\frac{EG}{PG}$=$\frac{PH}{FH}$,即$\frac{2-{x}_{2}}{{ax}_{2}^{2}-4a}$=$\frac{2-{x}_{1}}{-({ax}_{1}^{2}-4a)}$,
∴x1+x2=-4,
∴a=-$\frac{1}{2}$.
点评 本题综合考查了二次函数综合题,涉及的知识点有:待定系数法求二次函数解析式,勾股定理,相似三角形的判断与性质以及二次函数图象上点的坐标特征,方程思想,综合性较强,有一定的难度.

| A. | -5 | B. | 5 | C. | 0 | D. | 3 |
(1)某用户为了解日用电量,记录了4月第一周的用电量:
| 日 期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 用电量 (单位:度) | 5 | 7 | 8 | 6 | 4 | 5 | 7 |
(2)该用户到4月结束时去交电费,请问准备100元够吗?说明理由.
 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象信息解答:当出发几个小时后,两车相距为270km?
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象信息解答:当出发几个小时后,两车相距为270km?
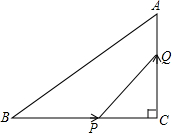 如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s的速度向点C移动,同时动点Q从C出发以1cm/s的速度向点A移动,设它们的运动时间为t.
如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s的速度向点C移动,同时动点Q从C出发以1cm/s的速度向点A移动,设它们的运动时间为t. 如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=$\sqrt{3}$,BC=1.连接BF,分别交AC、DC、DE与点P、Q、R.有下列结论①△BFG∽△ABC、②BQ=FQ、③AP=2PC、④EF平分∠BFG,你认为不正确的是④.
如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=$\sqrt{3}$,BC=1.连接BF,分别交AC、DC、DE与点P、Q、R.有下列结论①△BFG∽△ABC、②BQ=FQ、③AP=2PC、④EF平分∠BFG,你认为不正确的是④.