题目内容
3.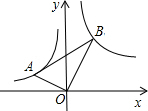 如图,在Rt△ABO中,∠AOB=90°,且OB=2AO,点A在反比例函数y=$-\frac{2}{x}$的图象上,点B比在反比例函数y=$\frac{m}{x}$的图象上,则m的值为( )
如图,在Rt△ABO中,∠AOB=90°,且OB=2AO,点A在反比例函数y=$-\frac{2}{x}$的图象上,点B比在反比例函数y=$\frac{m}{x}$的图象上,则m的值为( )| A. | 4 | B. | 6 | C. | -8 | D. | 8 |
分析 要求函数的解析式只要求出点B的坐标就可以,过点A,B作AC⊥x轴,BD⊥x轴,分别于C,D.根据条件得到△ACO∽△ODB,得到$\frac{AC}{OD}$=$\frac{OC}{BO}$=$\frac{AO}{OB}$=$\frac{1}{2}$求出OD=2b,BD=-2a,
得到B(2b,-2a),问题即可得解.
解答 解:设点A的坐标是(a,b),
因为点A在函数y=-$\frac{2}{x}$的图象上,则ab=-2,
则AC=B,OC=-a,
∵∠AOB=90°,
∴∠AOC+∠BOD=∠AOC+∠CAO=90°,
∠CAO=∠BOD,
∴△ACO∽△BDO,
∴$\frac{AC}{OD}$=$\frac{OC}{BO}$=$\frac{AO}{OB}$=$\frac{1}{2}$
∴OD=2b,BD=-2a,
∴B(2b,-2a),
∵点B比在反比例函数y=$\frac{m}{x}$的图象上,
∴2b•(-2a)=m,
∴m=8.
点评 本题考查了求函数的解析式的问题,相似三角形的判定和性质,能够把求反比例函数的解析式转化为求点的坐标的问题是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.为鼓励居民节约用电,某市电力公司规定了电费的分段计算的方法:每月用电不超过100度,按每度电0.50元计算;每月用电超过100度,超出部分按每度电0.65元计算.
(1)某用户为了解日用电量,记录了4月第一周的用电量:
请你估算该用户4月份30天的用电量约为多少度?
(2)该用户到4月结束时去交电费,请问准备100元够吗?说明理由.
(1)某用户为了解日用电量,记录了4月第一周的用电量:
| 日 期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 用电量 (单位:度) | 5 | 7 | 8 | 6 | 4 | 5 | 7 |
(2)该用户到4月结束时去交电费,请问准备100元够吗?说明理由.
18.计算3a3•(-a2)的结果是( )
| A. | 3a5 | B. | -3a5 | C. | 3a6 | D. | -3a6 |
 如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=$\sqrt{3}$,BC=1.连接BF,分别交AC、DC、DE与点P、Q、R.有下列结论①△BFG∽△ABC、②BQ=FQ、③AP=2PC、④EF平分∠BFG,你认为不正确的是④.
如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=$\sqrt{3}$,BC=1.连接BF,分别交AC、DC、DE与点P、Q、R.有下列结论①△BFG∽△ABC、②BQ=FQ、③AP=2PC、④EF平分∠BFG,你认为不正确的是④.