题目内容
18.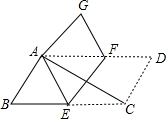 如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处,
如图,将平行四边形ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处,(1)求证:四边形AECF是菱形;
(2)连接AC,若平行四边形ABCD的面积为8,$\frac{EC}{BC}=\frac{2}{3}$,求AC•EF的值.
分析 (1)利用全等三角形的判定得出△AOF≌△COE(ASA),证得EO=FO,进而根据平行四边形的判定证得四边形AECF是平行四边形,因为AC⊥EF,即可证得四边形AECF是菱形;
(2)根据?ABCD与菱形AECF同高,$\frac{EC}{BC}=\frac{2}{3}$,进而得出?ABCD与菱形AECF的面积,进而根据菱形的面积等于两对角线乘积的一半即可得出答案.
解答 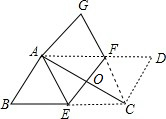 (1)证明:∵将?ABCD纸片沿EF折叠,使点C与点A重合,
(1)证明:∵将?ABCD纸片沿EF折叠,使点C与点A重合,
∴AO=CO,∠AOF=∠COE=90°,AD=BC,FG=DF,
在△AOF和△COE中.
$\left\{\begin{array}{l}{∠FAO=∠ECO}\\{AO=CO}\\{∠AOF=∠COE}\end{array}\right.$,
∴△AOF≌△COE(ASA),
∴EO=FO,
∵AO=CO,
∴四边形AECF是平行四边形,
∵AC⊥EF,
∴平行四边形AECF是菱形,
(2)解:∵?ABCD与菱形AECF同高,$\frac{EC}{BC}=\frac{2}{3}$,
∴?ABCD与菱形AECF的面积的比为:3:2,
∵平行四边形ABCD的面积为8,
∴菱形AECF的面积为$\frac{16}{3}$,
∵AC⊥EF,
∴菱形AECF的面积为:$\frac{1}{2}$×AC×EF=$\frac{16}{3}$,
∴AC•EF=$\frac{32}{3}$.
点评 此题主要考查了菱形的判定以及平行四边形的性质和全等三角形的判定与性质等知识,得出△AOF≌△COE是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
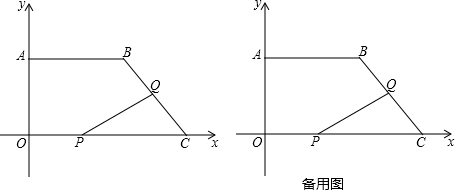

 如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=$\sqrt{3}$,BC=1.连接BF,分别交AC、DC、DE与点P、Q、R.有下列结论①△BFG∽△ABC、②BQ=FQ、③AP=2PC、④EF平分∠BFG,你认为不正确的是④.
如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=$\sqrt{3}$,BC=1.连接BF,分别交AC、DC、DE与点P、Q、R.有下列结论①△BFG∽△ABC、②BQ=FQ、③AP=2PC、④EF平分∠BFG,你认为不正确的是④. 如图所示,折叠矩形的一边AD,使点D落在BC上的点F处,已知:AB=8cm,BC=10cm.求EC的长.
如图所示,折叠矩形的一边AD,使点D落在BC上的点F处,已知:AB=8cm,BC=10cm.求EC的长.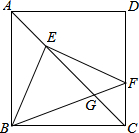 如图,已知,正方形ABCD的边长为1,点E、F分别在AC、DC上,若EC=BC,EF⊥BE,BF与EC交于G,则BG与GF的乘积为$3\sqrt{2}-4$.
如图,已知,正方形ABCD的边长为1,点E、F分别在AC、DC上,若EC=BC,EF⊥BE,BF与EC交于G,则BG与GF的乘积为$3\sqrt{2}-4$.