题目内容
13. 如图,在等腰直角三角形ABC中,∠A=90°,AB=AC=2,O为BC的中点,以O为圆心的圆弧分别与AB,AC相切于点D,E,则图中AD,AE与$\widehat{DE}$所围成的封闭图形的面积为1-$\frac{π}{4}$.
如图,在等腰直角三角形ABC中,∠A=90°,AB=AC=2,O为BC的中点,以O为圆心的圆弧分别与AB,AC相切于点D,E,则图中AD,AE与$\widehat{DE}$所围成的封闭图形的面积为1-$\frac{π}{4}$.
分析 首先连接OE,OD,由以O为圆心的圆弧分别与AB,AC相切于点D,E,易得四边形OEAD是正方形,然后由S阴影=S正方形OEAD-S扇形OED,求得答案.
解答 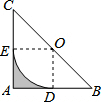 解:连接OE,OD,
解:连接OE,OD,
∵以O为圆心的圆弧分别与AB,AC相切于点D,E,
∴OE⊥AC,OD⊥AB,
∴∠OEA=∠ODA=∠A=90°,
∴四边形OEAD是矩形,
∵OE=OD,
∴四边形OEAD是正方形,
∵在等腰直角三角形ABC中,∠A=90°,AB=AC=2,O为BC的中点,
∴OE=$\frac{1}{2}$AB=1,
∴S阴影=S正方形OEAD-S扇形OED=1-$\frac{90×π×{1}^{2}}{360}$=1-$\frac{π}{4}$.
故答案为:1-$\frac{π}{4}$.
点评 此题考查了切线的性质、扇形的面积以及正方形的判定与性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
1.某艺术剧院门票价格如表所示:某团体准备了700元,全部用来购买指定日普通票和平日优惠票,且每种至少买一张.
门票价格一览表
(1)有多少种购票方案?列举所有可能结果;
(2)如果从上述方案中选中一种总票张数最少的情况,讲所购的票的票面朝下随意叠放在一起,随机抽两张,求正好抽出一张指定日普通票和一张平日优惠票的概率.
门票价格一览表
| 指定日普通票 | 200元 |
| 平日优惠票 | 100元 |
(2)如果从上述方案中选中一种总票张数最少的情况,讲所购的票的票面朝下随意叠放在一起,随机抽两张,求正好抽出一张指定日普通票和一张平日优惠票的概率.
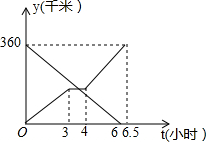 一辆货车从甲地向乙地行驶,一辆小轿车与该货车同时出发,从乙地向甲地行驶,货车匀速行驶至乙地,小轿车中途停车休整后提速行驶至甲地,货车与乙地的距离y1(千米)、小轿车与乙地的距离y2(千米)与行驶时间((小时)之间的函数关系的图象如图所示,已知当小轿车行驶2小时时,小轿车与货车相距140千米.
一辆货车从甲地向乙地行驶,一辆小轿车与该货车同时出发,从乙地向甲地行驶,货车匀速行驶至乙地,小轿车中途停车休整后提速行驶至甲地,货车与乙地的距离y1(千米)、小轿车与乙地的距离y2(千米)与行驶时间((小时)之间的函数关系的图象如图所示,已知当小轿车行驶2小时时,小轿车与货车相距140千米.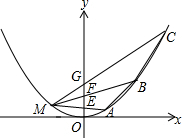 如图,M、A,B,C为抛物线y=ax2上不同的四点,M(-2,1),线段MA,MB,MC与y轴的交点分别为E,F,G.且EF=FG=1.
如图,M、A,B,C为抛物线y=ax2上不同的四点,M(-2,1),线段MA,MB,MC与y轴的交点分别为E,F,G.且EF=FG=1.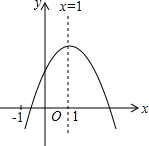 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列6个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤b2-4ac<0; ⑥a+b>m(am+b),(m≠1的实数)其中正确的结论有( )个.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列6个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤b2-4ac<0; ⑥a+b>m(am+b),(m≠1的实数)其中正确的结论有( )个. 如图,电信部门计划修建一条连接B、C两地电缆,测量人员在山脚A处测得B、C两处的仰角分别是37°和45°,在B处测得C处的仰角为67°.已知C地比A地髙330米(图中各点均在同一平面内),求电缆BC长至少多少米?(精确到米,参考数据:sin37°≈$\frac{3}{5}$,tan37°≈$\frac{3}{4}$,sin67°≈$\frac{12}{13}$,tan67°≈$\frac{12}{5}$)
如图,电信部门计划修建一条连接B、C两地电缆,测量人员在山脚A处测得B、C两处的仰角分别是37°和45°,在B处测得C处的仰角为67°.已知C地比A地髙330米(图中各点均在同一平面内),求电缆BC长至少多少米?(精确到米,参考数据:sin37°≈$\frac{3}{5}$,tan37°≈$\frac{3}{4}$,sin67°≈$\frac{12}{13}$,tan67°≈$\frac{12}{5}$)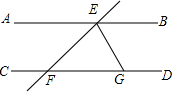 如图,平行线AB、CD被直线EF所截,过点E作EG⊥EF,与直线CD相交于点G,若∠AEF=39°,则∠EGF的度数为51°.
如图,平行线AB、CD被直线EF所截,过点E作EG⊥EF,与直线CD相交于点G,若∠AEF=39°,则∠EGF的度数为51°.