题目内容
4.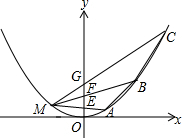 如图,M、A,B,C为抛物线y=ax2上不同的四点,M(-2,1),线段MA,MB,MC与y轴的交点分别为E,F,G.且EF=FG=1.
如图,M、A,B,C为抛物线y=ax2上不同的四点,M(-2,1),线段MA,MB,MC与y轴的交点分别为E,F,G.且EF=FG=1.(1)若F的坐标为(0,t),求点B的坐标(用t表示);
(2)若△AMB的面积是△BMC面积的$\frac{1}{2}$,求直线MB的解析式.
分析 (1)由点M在抛物线上,把坐标代入解析式求解,确定出抛物线解析式,设出点F(0,t)用t表示出直线MB的解析式即可;
(2)由(1)的方法确定出直线MG,ME的解析式,分别和抛物线联立求出交点坐标,用点到直线的距离公式求出距离,最后用面积关系确定出t值.
解答 解:(1)∵M(-2,1)为抛物线y=ax2上,
∴4a=1,
∴a=$\frac{1}{4}$,
∴抛物线解析式为y=$\frac{1}{4}$x2,
∵F的坐标为(0,t),
∴直线MB的解析式为y=$\frac{t-1}{2}$x+t,
∴抛物线解析式为y=$\frac{1}{4}$x2,
∴$\frac{1}{4}$x2=$\frac{t-1}{2}$x+t,
∴x=-2(舍)或x=2t,
∴B(2t,t2),
(2)∵EF=FG=1,F(0,t),
∴点E(0,t-1),G(0,t+1),
∵M(-2,1),
∴直线ME的解析式为y=$\frac{t-2}{2}$x+t-1①
直线MG的解析式为y=$\frac{t}{2}$x+t+1,②
∵抛物线解析式为y=$\frac{1}{4}$x2,③
联立①③得点A(2t-2,(t-1)2),
联立②③得点C(2t+2,(t+1)2),
∵直线MB的解析式为y=$\frac{t-1}{2}$x+t,
∴点A到直线MB的距离为d1=$\frac{|2(t-1)^{2}-2(t-1)^{2}+2t|}{\sqrt{(t-1)^{2}+4}}$=$\frac{2t}{\sqrt{{t}^{2}-2t+5}}$
点c到直线MB的距离为d2=$\frac{2t+4}{\sqrt{{t}^{2}-2t+5}}$,
∵△AMB的面积是△BMC面积的$\frac{1}{2}$,
∵$\frac{{S}_{△AMB}}{{S}_{△BMC}}$=$\frac{\frac{1}{2}MB×{d}_{1}}{\frac{1}{2}MB×{d}_{2}}$=$\frac{{d}_{1}}{{d}_{2}}$=$\frac{2t}{2t+4}$=$\frac{1}{2}$,
∴t=2,
∴直线MB的解析式为y=$\frac{1}{2}$x+2.
点评 此题是二次函数性质题,主要考查了函数关系式的确定和点到直线的距离公式,解本题的关键是用t表示出的交点坐标,难点是点到直线的距离公式的应用.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| 汽车行驶速度v(千米/小时) | 30 | 40 | 50 | 60 | 70 |
| 制动距离s(米) | 5 | 12 | 19 | 26 | 33 |
(2)若s是v的一次函数,求s关于v的函数解析式.
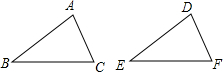 如图,给出下列四个条件,AB=DE,BC=EF,∠B=∠E,∠C=∠F,从中任选三个条件能使△ABC≌△DEF的共有( )
如图,给出下列四个条件,AB=DE,BC=EF,∠B=∠E,∠C=∠F,从中任选三个条件能使△ABC≌△DEF的共有( )| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
 已知A,B两地公路长300km,甲、乙两车同时从A地出发沿同一公路驶往B地,2小时后,甲车接到电话需返回这条公路上的C处取回货物,于是甲车立即原路返回C地,取了货物又立即赶往B地(取货物的时间忽略不计),结果两车同时到达B地.两车的速度始终保持不变,设两车出发xh后,甲、乙距离A地的距离分别为y1(km)和y2(km),它们的函数图象分别是折线OPQR和线段OR.
已知A,B两地公路长300km,甲、乙两车同时从A地出发沿同一公路驶往B地,2小时后,甲车接到电话需返回这条公路上的C处取回货物,于是甲车立即原路返回C地,取了货物又立即赶往B地(取货物的时间忽略不计),结果两车同时到达B地.两车的速度始终保持不变,设两车出发xh后,甲、乙距离A地的距离分别为y1(km)和y2(km),它们的函数图象分别是折线OPQR和线段OR. 如图,AD∥BC,AC2=AD•BC,求证;∠B=∠DCA.
如图,AD∥BC,AC2=AD•BC,求证;∠B=∠DCA.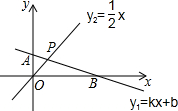 如图所示,已知直线y1=kx+b经过点(0,2),(-2,3),且与坐标轴交于点A、B两点.试:
如图所示,已知直线y1=kx+b经过点(0,2),(-2,3),且与坐标轴交于点A、B两点.试: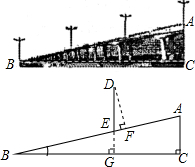 如图是某城市一座立交桥的引桥部分,桥面截面AB可以近似地看做Rt△ABC的斜边,桥面AB上路灯DE的高度为5m,已知坡角∠ABC为14°.
如图是某城市一座立交桥的引桥部分,桥面截面AB可以近似地看做Rt△ABC的斜边,桥面AB上路灯DE的高度为5m,已知坡角∠ABC为14°. 如图,在等腰直角三角形ABC中,∠A=90°,AB=AC=2,O为BC的中点,以O为圆心的圆弧分别与AB,AC相切于点D,E,则图中AD,AE与$\widehat{DE}$所围成的封闭图形的面积为1-$\frac{π}{4}$.
如图,在等腰直角三角形ABC中,∠A=90°,AB=AC=2,O为BC的中点,以O为圆心的圆弧分别与AB,AC相切于点D,E,则图中AD,AE与$\widehat{DE}$所围成的封闭图形的面积为1-$\frac{π}{4}$.