题目内容
5. 如图,电信部门计划修建一条连接B、C两地电缆,测量人员在山脚A处测得B、C两处的仰角分别是37°和45°,在B处测得C处的仰角为67°.已知C地比A地髙330米(图中各点均在同一平面内),求电缆BC长至少多少米?(精确到米,参考数据:sin37°≈$\frac{3}{5}$,tan37°≈$\frac{3}{4}$,sin67°≈$\frac{12}{13}$,tan67°≈$\frac{12}{5}$)
如图,电信部门计划修建一条连接B、C两地电缆,测量人员在山脚A处测得B、C两处的仰角分别是37°和45°,在B处测得C处的仰角为67°.已知C地比A地髙330米(图中各点均在同一平面内),求电缆BC长至少多少米?(精确到米,参考数据:sin37°≈$\frac{3}{5}$,tan37°≈$\frac{3}{4}$,sin67°≈$\frac{12}{13}$,tan67°≈$\frac{12}{5}$)
分析 过点C作经过点A的水平直线的垂线,垂足为点D,CD交过点B的水平直线于点E,过点B作BF⊥AD于点F,根据题意求出AD=CD,设AF=4x,利用正切的定义用x表示出BF,求出CE,根据正弦的定义列式计算即可.
解答 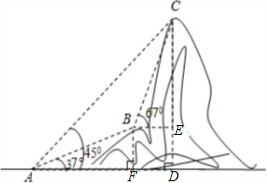 解:如图,过点C作经过点A的水平直线的垂线,垂足为点D,CD交过点B的水平直线于点E,
解:如图,过点C作经过点A的水平直线的垂线,垂足为点D,CD交过点B的水平直线于点E,
过点B作BF⊥AD于点F,则CD=330米,
∵∠CAD=45°
∴∠ACD=45°
∴AD=CD=330米,
设AF=4x,则BF=AF•tan37°≈4x•$\frac{3}{4}$=3x(米)
FD=(330-4x)米,
由四边形BEDF是矩形可得:BE=FD=(330-4x)米,ED=BF=3x米,
∴CE=CD-ED=(330-3x)米,
在Rt△BCE中,CE=BE•tan67°,
∴330-3x=(330-4x)×$\frac{12}{5}$,
解得x=70,
∴CE=330-3×70=120(米),
∴BC=$\frac{CE}{sin∠CBE}$=$\frac{120}{sin67°}$≈130(米)
答:电缆BC长至少130米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,正确理解仰角俯角的概念、灵活运用锐角三角函数的定义是解题的关键.

练习册系列答案
相关题目
20.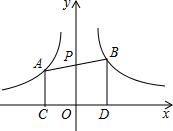 如图,直线分别与反比例函数y=-$\frac{2}{x}$和y=$\frac{3}{x}$的图象交于点A和点B,与y轴交于点P,且P为线段AB的中点,作AC⊥x轴于点C,BD⊥x于点D,则四边形ABDC的面积是( )
如图,直线分别与反比例函数y=-$\frac{2}{x}$和y=$\frac{3}{x}$的图象交于点A和点B,与y轴交于点P,且P为线段AB的中点,作AC⊥x轴于点C,BD⊥x于点D,则四边形ABDC的面积是( )
 如图,直线分别与反比例函数y=-$\frac{2}{x}$和y=$\frac{3}{x}$的图象交于点A和点B,与y轴交于点P,且P为线段AB的中点,作AC⊥x轴于点C,BD⊥x于点D,则四边形ABDC的面积是( )
如图,直线分别与反比例函数y=-$\frac{2}{x}$和y=$\frac{3}{x}$的图象交于点A和点B,与y轴交于点P,且P为线段AB的中点,作AC⊥x轴于点C,BD⊥x于点D,则四边形ABDC的面积是( )| A. | 3.5 | B. | 4 | C. | 4.5 | D. | 5 |
10.净水机的核心部件就是水处理反渗透膜,水处理反渗透膜就像是一个筛子,它的孔径只有0.11纳米,水在压力的作用下一层层过滤,离子以上的杂质像抗生素、重金属、细菌等都能过滤掉,0.11纳米即0.00000000011米,将0.11纳米用科学记数法表示为( )
| A. | 1.1×10-9米 | B. | 1.1×10-10米 | C. | 11×10-9米 | D. | 0.11×10-9米 |
14.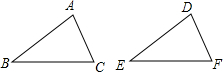 如图,给出下列四个条件,AB=DE,BC=EF,∠B=∠E,∠C=∠F,从中任选三个条件能使△ABC≌△DEF的共有( )
如图,给出下列四个条件,AB=DE,BC=EF,∠B=∠E,∠C=∠F,从中任选三个条件能使△ABC≌△DEF的共有( )
 如图,给出下列四个条件,AB=DE,BC=EF,∠B=∠E,∠C=∠F,从中任选三个条件能使△ABC≌△DEF的共有( )
如图,给出下列四个条件,AB=DE,BC=EF,∠B=∠E,∠C=∠F,从中任选三个条件能使△ABC≌△DEF的共有( )| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
 已知A,B两地公路长300km,甲、乙两车同时从A地出发沿同一公路驶往B地,2小时后,甲车接到电话需返回这条公路上的C处取回货物,于是甲车立即原路返回C地,取了货物又立即赶往B地(取货物的时间忽略不计),结果两车同时到达B地.两车的速度始终保持不变,设两车出发xh后,甲、乙距离A地的距离分别为y1(km)和y2(km),它们的函数图象分别是折线OPQR和线段OR.
已知A,B两地公路长300km,甲、乙两车同时从A地出发沿同一公路驶往B地,2小时后,甲车接到电话需返回这条公路上的C处取回货物,于是甲车立即原路返回C地,取了货物又立即赶往B地(取货物的时间忽略不计),结果两车同时到达B地.两车的速度始终保持不变,设两车出发xh后,甲、乙距离A地的距离分别为y1(km)和y2(km),它们的函数图象分别是折线OPQR和线段OR.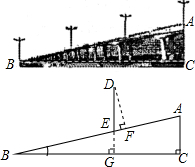 如图是某城市一座立交桥的引桥部分,桥面截面AB可以近似地看做Rt△ABC的斜边,桥面AB上路灯DE的高度为5m,已知坡角∠ABC为14°.
如图是某城市一座立交桥的引桥部分,桥面截面AB可以近似地看做Rt△ABC的斜边,桥面AB上路灯DE的高度为5m,已知坡角∠ABC为14°. 如图,在等腰直角三角形ABC中,∠A=90°,AB=AC=2,O为BC的中点,以O为圆心的圆弧分别与AB,AC相切于点D,E,则图中AD,AE与$\widehat{DE}$所围成的封闭图形的面积为1-$\frac{π}{4}$.
如图,在等腰直角三角形ABC中,∠A=90°,AB=AC=2,O为BC的中点,以O为圆心的圆弧分别与AB,AC相切于点D,E,则图中AD,AE与$\widehat{DE}$所围成的封闭图形的面积为1-$\frac{π}{4}$.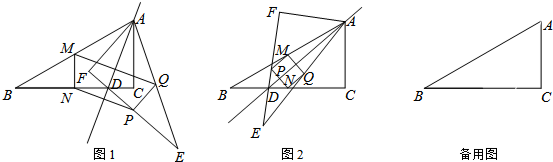
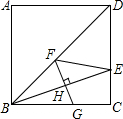 如图,正方形ABCD中,连接BD,在DC上取一点E,在BD上取一点F,使得∠BEC=∠DEF,过点F作FG⊥BE于H,交BC于G,若DE=5$\sqrt{6}$,GC=7,则CE=5$\sqrt{6}$-7.
如图,正方形ABCD中,连接BD,在DC上取一点E,在BD上取一点F,使得∠BEC=∠DEF,过点F作FG⊥BE于H,交BC于G,若DE=5$\sqrt{6}$,GC=7,则CE=5$\sqrt{6}$-7.