题目内容
3．
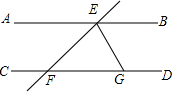如图，平行线AB、CD被直线EF所截，过点E作EG⊥EF，与直线CD相交于点G，若∠AEF=39°，则∠EGF的度数为51°．
分析 根据垂直的定义得到∠FEG=90°，根据平行线的性质得到∠EFG=∠AEF=39°，根据三角形的内角和即可得到结论．
解答 解：∵EG⊥EF，
∴∠FEG=90°，
∵AB∥CD，
∴∠EFG=∠AEF=39°，
∴∠EGF=51°，
故答案为：51．
点评 本题考查了平行线的性质，垂直定义，注意：①两直线平行，内错角相等，②两直线平行，同旁内角互补．
练习册系列答案
相关题目
如图，在等腰直角三角形ABC中，∠A=90°，AB=AC=2，O为BC的中点，以O为圆心的圆弧分别与AB，AC相切于点D，E，则图中AD，AE与$\widehat{DE}$所围成的封闭图形的面积为1-$\frac{π}{4}$．
14．
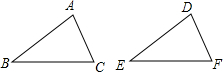如图，给出下列四个条件，AB=DE，BC=EF，∠B=∠E，∠C=∠F，从中任选三个条件能使△ABC≌△DEF的共有（ ）
如图，给出下列四个条件，AB=DE，BC=EF，∠B=∠E，∠C=∠F，从中任选三个条件能使△ABC≌△DEF的共有（ ）| A． | 1组 | B． | 2组 | C． | 3组 | D． | 4组 |
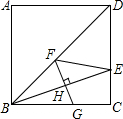如图，正方形ABCD中，连接BD，在DC上取一点E，在BD上取一点F，使得∠BEC=∠DEF，过点F作FG⊥BE于H，交BC于G，若DE=5$\sqrt{6}$，GC=7，则CE=5$\sqrt{6}$-7．
13．$\sqrt{2x-3}$在实数范围内有意义，则x的取值范围是（ ）
| A． | x≥$\frac{3}{2}$ | B． | x＞$\frac{3}{2}$ | C． | x≤$\frac{3}{2}$ | D． | x＜$\frac{3}{2}$ |