题目内容
19.在学习“约分和通分”时,小明和小华都遇到了“化简$\frac{{x}^{2}-{y}^{2}}{x+y}$”这道题.小明的解法是:$\frac{{x}^{2}-{y}^{2}}{x+y}$=$\frac{(x-y)(x+y)}{x+y}$=x-y
小华的解法是:$\frac{{x}^{2}-{y}^{2}}{x+y}$=$\frac{({x}^{2}-{y}^{2})(x-y)}{(x+y)(x-y)}$=$\frac{({x}^{2}-{y}^{2})(x-y)}{{x}^{2}-{y}^{2}}$=x-y
如果你与小明、小华在一个学习小组,请你发表一下自己的意见.
分析 小明的解题方法正确.运用分式的性质解题时,注意分子、分母同时乘以(x-y)的前提是x-y≠0.
解答 解:小明的解法正确.理由如下:
小华的解法是:$\frac{{x}^{2}-{y}^{2}}{x+y}$=$\frac{({x}^{2}-{y}^{2})(x-y)}{(x+y)(x-y)}$=$\frac{({x}^{2}-{y}^{2})(x-y)}{{x}^{2}-{y}^{2}}$=x-y
这里分子、分母同时乘以(x-y),若x-y=0时,该方法不合适.
点评 本题考查了通分、平方差公式,约分.运用分式的性质解题时,注意分式的分母不等于零.

练习册系列答案
相关题目
8.若|a|>-a,则( )
| A. | a>0 | B. | a<0 | C. | a<-1 | D. | 1<a |
6.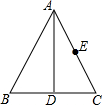 如图,在等边△ABC中,AD平分∠BAC交BC与点D,点E为AC边的中点,BC=2;在AD上有一动点Q,则QC+QE的最小值为( )
如图,在等边△ABC中,AD平分∠BAC交BC与点D,点E为AC边的中点,BC=2;在AD上有一动点Q,则QC+QE的最小值为( )
 如图,在等边△ABC中,AD平分∠BAC交BC与点D,点E为AC边的中点,BC=2;在AD上有一动点Q,则QC+QE的最小值为( )
如图,在等边△ABC中,AD平分∠BAC交BC与点D,点E为AC边的中点,BC=2;在AD上有一动点Q,则QC+QE的最小值为( )| A. | $\sqrt{3}$ | B. | 1.5 | C. | $\sqrt{2}$ | D. | 1 |
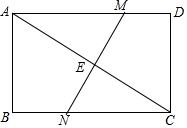 如图,在矩形ABCD中,AC是对角线,AC的中垂线MN交AD于M,交BC于N,AB=6,BC=8,求MN的长.
如图,在矩形ABCD中,AC是对角线,AC的中垂线MN交AD于M,交BC于N,AB=6,BC=8,求MN的长.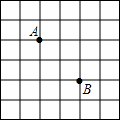 如图,A,B在格点位置上,若要在所给的网络中再找一个格点,使它与点A,B连成的三角形是轴对称图形,那么图中满足这样条件的格点格点共有( )
如图,A,B在格点位置上,若要在所给的网络中再找一个格点,使它与点A,B连成的三角形是轴对称图形,那么图中满足这样条件的格点格点共有( )