题目内容
10.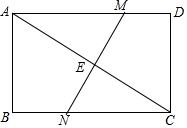 如图,在矩形ABCD中,AC是对角线,AC的中垂线MN交AD于M,交BC于N,AB=6,BC=8,求MN的长.
如图,在矩形ABCD中,AC是对角线,AC的中垂线MN交AD于M,交BC于N,AB=6,BC=8,求MN的长.
分析 由勾股定理可求得AC=10,由翻折的性质可知:EA=EC=5,AC⊥MN,然后根据△EAM∽△BCA,从而可求得EM的长,由此即可解决问题.
解答 解:(1)在Rt△ABC中,由勾股定理得:AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
由翻折的性质可知:EA=EC=5,AC⊥MN.
∵∠AEM=∠B=90°,∠EAM=∠BCA,
∴△EAM∽△BCA.
∴$\frac{EA}{BC}$=$\frac{EM}{AB}$,即$\frac{5}{8}$=$\frac{EM}{6}$.
解得:EM=$\frac{15}{4}$,同理可得EN=$\frac{15}{4}$,
∴MN=$\frac{15}{2}$.
点评 本题主要考查的是翻折的性质、相似三角形的性质和判定、勾股定理的应用,掌握相关定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列说法正确的是( )
| A. | x的系数为0 | B. | $\frac{1}{a}$是单项式 | C. | 1是单项式 | D. | -4x系数是4 |
18.如果分式$\frac{1}{1-x}$无意义,那么x的取值范围是( )
| A. | x>1 | B. | x<1 | C. | x≠1 | D. | x=1 |
17.已知二次函数y=x2-4mx+m-$\frac{1}{2}$的图象经过原点O,与x轴相交于另一点A,抛物线的顶点为B,则△OAB的面积是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{3}{2}$ |