题目内容
9. 如图,五边形ABCDE中,AB=AE,BC=ED,O为CD的中点,连接BO,EO,BO=EO,试探索AO与CD的位置关系.
如图,五边形ABCDE中,AB=AE,BC=ED,O为CD的中点,连接BO,EO,BO=EO,试探索AO与CD的位置关系.
分析 根据SSS判定△ABO≌△AEO,△BCO≌△EDO,结论即可得出.
解答 解:AO⊥CD,
理由:在△ABO与△AEO中,$\left\{\begin{array}{l}{AB=AE}\\{BO=EO}\\{AO=AO}\end{array}\right.$,
∴△ABO≌△AEO,
∴∠AOB=∠AOE,
∵O为CD的中点,
∴OC=OD,
在△BCO与△EDO中,$\left\{\begin{array}{l}{BO=EO}\\{BC=ED}\\{OC=OD}\end{array}\right.$,
∴∠BOC=∠EOD,
∴∠AOB+∠BOC=∠AOE+∠EOD,
即∠AOC=∠AOD,
∵∠AOC+∠AOD=180°,
∴∠AOC=∠AOD=90°,
∴AO⊥CD.
点评 本题考查了全等三角形的判定和性质,垂直的定义,熟练掌握全等三角形的判定和性质定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.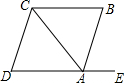 如图,点E在DA的延长线上,下列条件中能判定AB∥CD的是( )
如图,点E在DA的延长线上,下列条件中能判定AB∥CD的是( )
 如图,点E在DA的延长线上,下列条件中能判定AB∥CD的是( )
如图,点E在DA的延长线上,下列条件中能判定AB∥CD的是( )| A. | ∠B=∠BAE | B. | ∠BCA=∠CAD | C. | ∠BCA+∠CAE=180° | D. | ∠D=∠BAE |
14. 如图,直线AB与CD相交于O,E是∠AOD内一点,已知EO⊥AB,垂足为O,且∠BOD=45°,则∠COE的度数是( )
如图,直线AB与CD相交于O,E是∠AOD内一点,已知EO⊥AB,垂足为O,且∠BOD=45°,则∠COE的度数是( )
 如图,直线AB与CD相交于O,E是∠AOD内一点,已知EO⊥AB,垂足为O,且∠BOD=45°,则∠COE的度数是( )
如图,直线AB与CD相交于O,E是∠AOD内一点,已知EO⊥AB,垂足为O,且∠BOD=45°,则∠COE的度数是( )| A. | 115° | B. | 125° | C. | 135° | D. | 145° |
18.已知边长为m的正方形面积为12,则下列关于m的说法中,错误的是( )
①m是无理数;
②m是方程m2-12=0的解;
③m满足不等式组$\left\{\begin{array}{l}{m-4>0}\\{m-5<0}\end{array}\right.$;
④m是12的算术平方根.
①m是无理数;
②m是方程m2-12=0的解;
③m满足不等式组$\left\{\begin{array}{l}{m-4>0}\\{m-5<0}\end{array}\right.$;
④m是12的算术平方根.
| A. | ①② | B. | ①③ | C. | ③ | D. | ①②④ |
2.某手机专卖店销售A,B两种型号的手机,如表是近两周的销售情况:
(1)求每台A型手机和B型手机的销售利润;
(2)该手机专卖店计划一次购进两种型号的手机共100台,其中A型号手机的进货量不超过B型号手机进货量的2倍.设购进A型号手机x台,这100台手机的销售总利润为y元.
①求y关于x的函数表达式;
②该商店购进A型号和B型号手机各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型号手机的出厂价提高a(0<a<100)元,对B型号手机的出厂价下降a(0<a<100)元,且限定该手机专卖店至少购进A型号手机20台.若该手机专卖店保持两种手机的售价不变,请根据以上信息及(2)中条件,设计出使这100台手机销售总利润最大的进货方案.
| 销售时段 | 销售数量 | 销售利润 | |
| A型 | B型 | ||
| 第一周 | 3台 | 5台 | 1800元 |
| 第二周 | 4台 | 10台 | 3000元 |
(2)该手机专卖店计划一次购进两种型号的手机共100台,其中A型号手机的进货量不超过B型号手机进货量的2倍.设购进A型号手机x台,这100台手机的销售总利润为y元.
①求y关于x的函数表达式;
②该商店购进A型号和B型号手机各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型号手机的出厂价提高a(0<a<100)元,对B型号手机的出厂价下降a(0<a<100)元,且限定该手机专卖店至少购进A型号手机20台.若该手机专卖店保持两种手机的售价不变,请根据以上信息及(2)中条件,设计出使这100台手机销售总利润最大的进货方案.
 如图,一个小正方形网格的边长表示50米.A同学上学时从家中出发,先向东走250米,再向北走50米就到达学校.
如图,一个小正方形网格的边长表示50米.A同学上学时从家中出发,先向东走250米,再向北走50米就到达学校.
 如图,AC与BD相交于点O,且AB=CD,请添加一个条件∠A=∠C,使得△ABO≌△CDO.
如图,AC与BD相交于点O,且AB=CD,请添加一个条件∠A=∠C,使得△ABO≌△CDO.