题目内容
7.古希腊数学家把数1,3,6,10,15,21…叫做三角形数,它有一定的规律性,若把第一个三角形数记为a1,第二个三角形数记为a2,…,第n个三角形数记为an,计算a2-a1,a3-a2,a4-a3,…,由此推算,a100-a99=100,an=$\frac{1}{2}$n(n+1).分析 相邻两个数相减等于前面数的下标,如:an-an-1=n.利用(a2-a1)+(a3-a2)+(a4-a3)+…+(an-an-1)=an-a1,求an.
解答 解:a2-a1=3-1=2;
a3-a2=6-3=3;
a4-a3=10-6=4;
…;
an-an-1=n.
所以a100-a99=100.
an=an-1+n=$\frac{1}{2}$n(n+1).
故答案为:100,$\frac{1}{2}$n(n+1).,
点评 此题考查数字的变化规律,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的,找出规律解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14. 如图,直线AB与CD相交于O,E是∠AOD内一点,已知EO⊥AB,垂足为O,且∠BOD=45°,则∠COE的度数是( )
如图,直线AB与CD相交于O,E是∠AOD内一点,已知EO⊥AB,垂足为O,且∠BOD=45°,则∠COE的度数是( )
 如图,直线AB与CD相交于O,E是∠AOD内一点,已知EO⊥AB,垂足为O,且∠BOD=45°,则∠COE的度数是( )
如图,直线AB与CD相交于O,E是∠AOD内一点,已知EO⊥AB,垂足为O,且∠BOD=45°,则∠COE的度数是( )| A. | 115° | B. | 125° | C. | 135° | D. | 145° |
15. 如图,探索下列规律,根据规律,从2014到2016箭头的方向是( )
如图,探索下列规律,根据规律,从2014到2016箭头的方向是( )
 如图,探索下列规律,根据规律,从2014到2016箭头的方向是( )
如图,探索下列规律,根据规律,从2014到2016箭头的方向是( )| A. | ↓→ | B. | →↑ | C. | ↑→ | D. | →↓ |
2.某手机专卖店销售A,B两种型号的手机,如表是近两周的销售情况:
(1)求每台A型手机和B型手机的销售利润;
(2)该手机专卖店计划一次购进两种型号的手机共100台,其中A型号手机的进货量不超过B型号手机进货量的2倍.设购进A型号手机x台,这100台手机的销售总利润为y元.
①求y关于x的函数表达式;
②该商店购进A型号和B型号手机各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型号手机的出厂价提高a(0<a<100)元,对B型号手机的出厂价下降a(0<a<100)元,且限定该手机专卖店至少购进A型号手机20台.若该手机专卖店保持两种手机的售价不变,请根据以上信息及(2)中条件,设计出使这100台手机销售总利润最大的进货方案.
| 销售时段 | 销售数量 | 销售利润 | |
| A型 | B型 | ||
| 第一周 | 3台 | 5台 | 1800元 |
| 第二周 | 4台 | 10台 | 3000元 |
(2)该手机专卖店计划一次购进两种型号的手机共100台,其中A型号手机的进货量不超过B型号手机进货量的2倍.设购进A型号手机x台,这100台手机的销售总利润为y元.
①求y关于x的函数表达式;
②该商店购进A型号和B型号手机各多少台,才能使销售总利润最大?
(3)实际进货时,厂家对A型号手机的出厂价提高a(0<a<100)元,对B型号手机的出厂价下降a(0<a<100)元,且限定该手机专卖店至少购进A型号手机20台.若该手机专卖店保持两种手机的售价不变,请根据以上信息及(2)中条件,设计出使这100台手机销售总利润最大的进货方案.
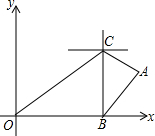 中国派遣三艘海监船在南海保护中国渔民不受菲律宾的侵犯.在雷达显示图上,标明了三艘海监船的坐标为O(0,0)、B(80,0)、C(80,60),(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域(只考虑在海平面上的探测).
中国派遣三艘海监船在南海保护中国渔民不受菲律宾的侵犯.在雷达显示图上,标明了三艘海监船的坐标为O(0,0)、B(80,0)、C(80,60),(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为r的圆形区域(只考虑在海平面上的探测).