题目内容
3.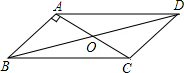 如图,在?ABCD中,对角线AC,BD交于点O,AB⊥AC,∠DAC=45°,AC=2,求BD的长.
如图,在?ABCD中,对角线AC,BD交于点O,AB⊥AC,∠DAC=45°,AC=2,求BD的长.
分析 首先根据平行四边形的性质得到△ACD是等腰直角三角形,从而求得AB和AO的长,利用勾股定理求得BO的长即可求得对角线BD的长.
解答 解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AB⊥AC,
∴∠ACD=∠BAC=90°,
∵∠DAC=45°,AC=2,
∴AB=CD=2,
∵AO=$\frac{1}{2}$AC=1,
∴由勾股定理得:BO=$\sqrt{3}$,
∴BD=2BO=2$\sqrt{3}$.
点评 本题考查了平行四边形的性质及勾股定理的知识,解题的关键是牢记:平行四边形的对角线互相平分,难度不大.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
14. 如图,直线AB、CD被直线EF所截,则∠3的内错角是( )
如图,直线AB、CD被直线EF所截,则∠3的内错角是( )
 如图,直线AB、CD被直线EF所截,则∠3的内错角是( )
如图,直线AB、CD被直线EF所截,则∠3的内错角是( )| A. | ∠1 | B. | ∠2 | C. | ∠4 | D. | ∠5 |
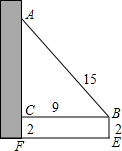 一幢高层住宅楼发生火灾,消防车立即赶到,在距住宅楼9米的B处升起梯搭在火灾窗口(如图),已知云梯长15米,云梯底部距地面2米,发生火灾的住户窗口A离地面有14米.
一幢高层住宅楼发生火灾,消防车立即赶到,在距住宅楼9米的B处升起梯搭在火灾窗口(如图),已知云梯长15米,云梯底部距地面2米,发生火灾的住户窗口A离地面有14米.
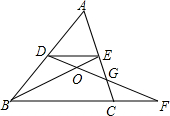 如图所示,在三角形ABC中,点D、E分别是边AB、AC的中点,DF过EC的中点G并与BC的延长线交于点F,BE与DE交于点O.若△ADE的面积为2,则四边形BOGC的面积为$\frac{7}{2}$.
如图所示,在三角形ABC中,点D、E分别是边AB、AC的中点,DF过EC的中点G并与BC的延长线交于点F,BE与DE交于点O.若△ADE的面积为2,则四边形BOGC的面积为$\frac{7}{2}$.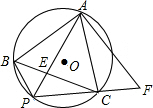 如图,正三角形ABC内接于⊙O,P是BC上的一点,且PB<PC,PA交BC于E,点F是PC延长线上的点,CF=PB,AB=$\sqrt{13}$,PA=4.
如图,正三角形ABC内接于⊙O,P是BC上的一点,且PB<PC,PA交BC于E,点F是PC延长线上的点,CF=PB,AB=$\sqrt{13}$,PA=4.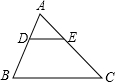 如图,在△ABC中,$\frac{AD}{DB}$=$\frac{AE}{EC}$=$\frac{1}{2}$,若△ADE的面积为1,则四边形DBCE的面积为( )
如图,在△ABC中,$\frac{AD}{DB}$=$\frac{AE}{EC}$=$\frac{1}{2}$,若△ADE的面积为1,则四边形DBCE的面积为( ) 如图,在△ABC中,AB=AC,AD=DB=BC,DE⊥AB于点E,若CD=4,且△BDC的周长为24,求AE的长.
如图,在△ABC中,AB=AC,AD=DB=BC,DE⊥AB于点E,若CD=4,且△BDC的周长为24,求AE的长.