题目内容
1.计算:32013×(-$\frac{1}{3}$)2014=$\frac{1}{3}$.分析 首先把(-$\frac{1}{3}$)2014化成(-$\frac{1}{3}$)2013×(-$\frac{1}{3}$),然后应用乘法结合律,求出32013×(-$\frac{1}{3}$)2013的值是多少;然后用它和-$\frac{1}{3}$相乘,求出算式32013×(-$\frac{1}{3}$)2014的值是多少即可.
解答 解:32013×(-$\frac{1}{3}$)2014
=32013×[(-$\frac{1}{3}$)2013×(-$\frac{1}{3}$)]
=32013×(-$\frac{1}{3}$)2013×(-$\frac{1}{3}$)
=[3×(-$\frac{1}{3}$)]2013×(-$\frac{1}{3}$)
=(-1)2013×(-$\frac{1}{3}$)
=(-1)×(-$\frac{1}{3}$)
=$\frac{1}{3}$
故答案为:$\frac{1}{3}$.
点评 此题主要考查了幂的乘方法则和积的乘方法则,以及乘法运算定律的应用,要熟练掌握,解答此题的关键是把(-$\frac{1}{3}$)2014化成(-$\frac{1}{3}$)2013×(-$\frac{1}{3}$),进而根据乘法结合律,求出32013×(-$\frac{1}{3}$)2013的值是多少.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
12.一辆汽车在笔直的公路上行驶,两次拐弯后,在原来的反方向上平行行驶,那么汽车两次拐弯的角度是( )
| A. | 第一次右拐60°,第二次左拐120° | B. | 第一次左拐70°,第二次右拐70° | ||
| C. | 第一次左拐65°,第二次左拐115° | D. | 第一次右拐50°,第二次右拐50° |
9.已知OC是∠AOB的平分线,下列结论不正确的是( )
| A. | ∠AOB=$\frac{1}{2}$∠BOC | B. | ∠AOC=$\frac{1}{2}$∠AOB | C. | ∠AOC=∠BOC | D. | ∠AOB=2∠AOC |
16.下列说法正确的是( )
| A. | 延长直线AB | |
| B. | 线段AB和线段BA不是同一条线段 | |
| C. | 两点确定一条直线 | |
| D. | 连接两点间的线段叫做两点间的距离 |
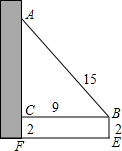 一幢高层住宅楼发生火灾,消防车立即赶到,在距住宅楼9米的B处升起梯搭在火灾窗口(如图),已知云梯长15米,云梯底部距地面2米,发生火灾的住户窗口A离地面有14米.
一幢高层住宅楼发生火灾,消防车立即赶到,在距住宅楼9米的B处升起梯搭在火灾窗口(如图),已知云梯长15米,云梯底部距地面2米,发生火灾的住户窗口A离地面有14米.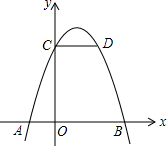 如图,在平面直角坐标系中,抛物线y=a(x-1)2+k(a、k为常数)与x轴交于点A、B,与y轴交于点C,CD∥x轴,与抛物线交于点D.若点A的坐标为(-1,0),则线段OB与线段CD的长度和为5.
如图,在平面直角坐标系中,抛物线y=a(x-1)2+k(a、k为常数)与x轴交于点A、B,与y轴交于点C,CD∥x轴,与抛物线交于点D.若点A的坐标为(-1,0),则线段OB与线段CD的长度和为5.