题目内容
10.(1)计算:4sin60°-|3-$\sqrt{12}$|+( $\frac{1}{2}$)-2;(2)解方程:x2-$\sqrt{3}$x-$\frac{1}{4}$=0.
分析 (1)本题涉及负整数指数幂、二次根式化简、绝对值、特殊角的三角函数值四个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果;
(2)利用配方法或公式法解答此题,均可得结果.
解答 解:(1)原式=2$\sqrt{3}$-2$\sqrt{3}$+3+4
=7;
(2)方法一:移项,得x2-$\sqrt{3}$x=$\frac{1}{4}$,
配方,得(x-$\frac{\sqrt{3}}{2}$)2=1
由此可得x-$\frac{\sqrt{3}}{2}$=±1,
x1=1+$\frac{\sqrt{3}}{2}$,x2=-1+$\frac{\sqrt{3}}{2}$
方法二:a=1,b=-$\sqrt{3}$,c=-$\frac{1}{4}$.
△=b2-4ac=(-$\sqrt{3}$)2-4×1×(-$\frac{1}{4}$)=4>0
方程有两个不等的实数根
x=$\frac{-b±\sqrt{b2-4ac}}{2a}$=$\frac{\sqrt{3}±\sqrt{4}}{2×1}$=$\frac{\sqrt{3}}{2}$±1,
x1=1+$\frac{\sqrt{3}}{2}$,x2=-1+$\frac{\sqrt{3}}{2}$
点评 本题考查实数的综合运算和一元二次方程的解法,解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负整数指数幂的运算、二次根式化简、绝对值等考点的运算以及公式法和配方法的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
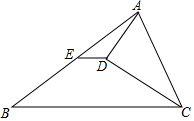 已知,如图所示,在△ABC中,E是AB的中点,CD平分∠ACB,AD⊥CD于点D,连接ED,求证:
已知,如图所示,在△ABC中,E是AB的中点,CD平分∠ACB,AD⊥CD于点D,连接ED,求证: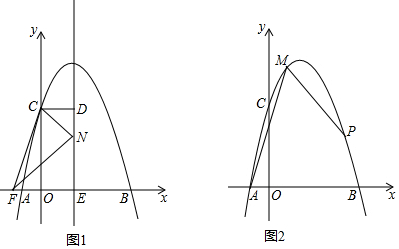
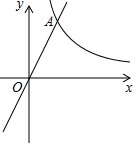 已知:如图,在平面直角坐标系xOy中,反比例函数y=$\frac{8}{x}$的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0).
已知:如图,在平面直角坐标系xOy中,反比例函数y=$\frac{8}{x}$的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0).


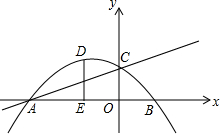 如图,抛物线y=ax2+bx+1与直线y=-ax+c相交于坐标轴上点A(-3,0),C(0,1)两点.
如图,抛物线y=ax2+bx+1与直线y=-ax+c相交于坐标轴上点A(-3,0),C(0,1)两点.