题目内容
14．下列方程中，解是x=2的方程是（ ）| A． | 3x+6=0 | B． | $\frac{1}{2}$-$\frac{1}{4}$x=0 | C． | $\frac{2}{3}$x=3 | D． | 5-3x=1 |
分析 根据方程的解得概念即可判断．
解答 解：（A）左边=12，右边=0，左边≠右边，故x=2不是3x+6=0的解；
（B）左边=0，右边=0，左边=右边，故x=2是$\frac{1}{2}$-$\frac{1}{4}x$=0的解；
（C）左边=$\frac{4}{3}$，右边=3，左边≠右边，故x=2不是$\frac{2}{3}$x=3的解；
（D）左边=-1，右边=1，左边≠右边，故x=2不是5-3x=1的解；
故选（B）
点评 本题考查方程的解，解题的关键是正确理解方程的解的概念，本题属于基础题型．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
5．
某中学为了响应国家发展足球的战略方针，激发学生对足球的兴趣，特举办全员参与的“足球比赛”，赛后，全校随机抽查部分学生，其成绩（百分制）整理分成5组，并制成如下频数分布表和扇形统计图，请根据所提供的信息解答下列问题：
成绩频数分布表
（1）频数分布表中的m=4，n=18；
（2）样本中位数所在成绩的级别是D，扇形统计图中，E组所对应的扇形圆心角的度数是108；
（3）若该校共有2000名学生，请你估计体育综合测试成绩不少于80分的大约有多少人？
某中学为了响应国家发展足球的战略方针，激发学生对足球的兴趣，特举办全员参与的“足球比赛”，赛后，全校随机抽查部分学生，其成绩（百分制）整理分成5组，并制成如下频数分布表和扇形统计图，请根据所提供的信息解答下列问题：成绩频数分布表
| 组别 | 成绩（分） | 频数 |
| A | 50≤x＜60 | 6 |
| B | 60≤x＜70 | m |
| C | 70≤x＜80 | 20 |
| D | 80≤x＜90 | 36 |
| E | 90≤x＜100 | n |
（2）样本中位数所在成绩的级别是D，扇形统计图中，E组所对应的扇形圆心角的度数是108；
（3）若该校共有2000名学生，请你估计体育综合测试成绩不少于80分的大约有多少人？
2．
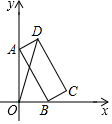如图，矩形ABCD中，AB=8，BC=3，顶点A，B分别在y轴和x轴上，当点A在y轴上移动时，点B也随之在x轴上移动，在移动过程中，OD的最大值为（ ）
如图，矩形ABCD中，AB=8，BC=3，顶点A，B分别在y轴和x轴上，当点A在y轴上移动时，点B也随之在x轴上移动，在移动过程中，OD的最大值为（ ）| A． | 8 | B． | $\sqrt{73}$ | C． | $\sqrt{85}$ | D． | 9 |
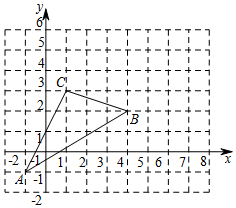如图，△ABC在直角坐标系中，