题目内容

3．如图，△ABC在直角坐标系中，
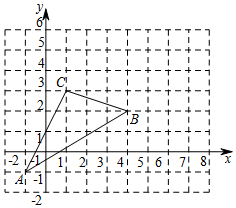
（1）写出△ABC各点的坐标．A（-1，-1）B（4，2）C（1，3）．
（2）若把△ABC向上平移1个单位，再向右平移3个单位得△A′B′C′，在图中画出△A′B′C′，并写出A′、B′、C′的坐标．A′（2，0）B′（7，3）C′（4，4）．
（3）连结CA′，CB′，则△CA′B′的面积是5．

分析 （1）由图形可得；
（2）画出平移后的三角形，根据图形可得；
（3）割补法求解可得．

解答 解：（1）由图形可知△ABC各点的坐标如下：A（-1，-1）、B（4，2）、C（1，3），
故答案为：-1、-1、4、2、1、3；

（2）平移后△A′B′C′如图所示，

则A′（2，0）、B′（7，3）、C′（4，4），
故答案为：2、0、7、3、4、4；

（3）△CA′B′的面积是3×4-$\frac{1}{2}$×1×3-$\frac{1}{2}$×2×4-$\frac{1}{2}$×1×3=5，
故答案为：5．

点评 本题主要考查作图-平移变换，熟练掌握平移的定义和性质是解题的关键．

练习册系列答案
相关题目
13．（1）计算：$（\frac{1}{2}）^{-2}-6sin30°-（\frac{1}{\sqrt{7}}）^{0}+\sqrt{2}+|\sqrt{2}-\sqrt{3}|$．
（2）解不等式组：$\left\{\begin{array}{l}{x+4≤3（x+2）}\\{\frac{x-1}{2}＜\frac{x}{3}}\end{array}\right.$．
14．下列方程中，解是x=2的方程是（　　）
A．3x+6=0B．$\frac{1}{2}$-$\frac{1}{4}$x=0C．$\frac{2}{3}$x=3D．5-3x=1
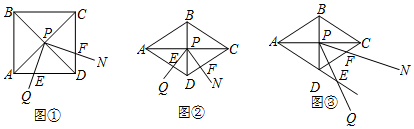
11．顺次连接对角线互相垂直的四边形的各边中点，所得图形一定是（　　）
A．正方形B．矩形C．菱形D．直角梯形
18．如图①，∠QPN的顶点P在正方形ABCD两条对角线的交点处，∠QPN=α，∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F（点F与点C、D不重合）．

（1）如图①，当α=90°时，求证：DE+DF=AD．
（2）如图②，将图①中的正方形ABCD改为∠ADC=120°的菱形，其他条件不变，当α=60°时，（1）中的结论变为$DE+DF=\frac{1}{2}AD$，请给出证明．
（3）在（2）的条件下，将∠QPN绕点P旋转，若旋转过程中∠QPN的边PQ与边AD的延长线交于点E，其他条件不变，探究在整个运动变化过程中，DE，DF，AD之间满足的数量关系，直接写出结论，不用加以证明．
8．如图1，某超市从一楼到二楼的电梯AB的长为18米，电梯每级的水平级宽是0.3米．竖直级高是$\frac{\sqrt{3}}{10}$米．
（1）求该电梯的坡角∠BAC的度数．
（2）若电梯以每秒上升2级的速度运行，求小明跨上电梯从一楼上升到二楼需要的时间．
15．下列各式中，正确的是（　　）
A．m2•m3=m6B．（2a+b）（a-b）=2a2+ab-b2
C．（5a+2b）（5a-3b）=25a2-6b2D．（x-y）（x2+xy+y2）=x3-y3
12．如图所示，在每个边长都为1的小正方形组成的网格中，点A、B、C均为格点．
（Ⅰ）线段AB的长度等于5；
（Ⅱ）若P为线段AB上的动点，以PC、PA为邻边的四边形PAQC为平行四边形，当PQ长度最小时，请你借助网格和无刻度的直尺画出该平行四边形，并简要说明你的作图方法（不要求证明）．
13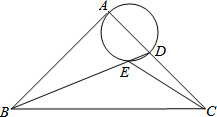．如图，在等腰直角△ABC中，∠BAC=90°，AB=AC，BC=4$\sqrt{2}$，点D是AC上一动点，连接BD，以AD为直径的圆交BD于点E，则线段CE长度的最小值是（　　）
A．2B．4C．$2\sqrt{2}-2$D．$2\sqrt{5}-2$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网