题目内容
4.定义:在平面直角坐标系中,点A、B为函数L图象上的任意两点,点A坐标为(x1,y1),点B坐标为(x2,y2),把式子$\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}$称为函数L从x1到x2的平均变化率;对于函数K:y=2x2-3x+1图象上有两点A(x1,y1)和B(x2,y2),当x1=1,x2-x1=$\frac{1}{3}$时,函数K从x1到x2的平均变化率是$\frac{5}{3}$;当x1=1,x2-x1=$\frac{1}{n}$(n为正整数)时,函数K从x1到x2的平均变化率是$\frac{n+2}{n}$.分析 先求出x2的值,再求出y1、y2,根据新定义求解可得.
解答 解:∵x1=1,x2-x1=$\frac{1}{3}$,
∴x2=$\frac{4}{3}$,
则y1=0,y2=2×$\frac{16}{9}$-3×$\frac{4}{3}$+1=$\frac{5}{9}$,
∴函数K从x1到x2的平均变化率是$\frac{\frac{5}{9}-0}{\frac{1}{3}}$=$\frac{5}{3}$;
∵x1=1,x2-x1=$\frac{1}{n}$,
∴x2=$\frac{n+1}{n}$,
则y1=0,y2=2×$\frac{(n+1)^{2}}{{n}^{2}}$-3×$\frac{n+1}{n}$+1=$\frac{n+2}{{n}^{2}}$,
∴函数K从x1到x2的平均变化率是$\frac{\frac{n+2}{{n}^{2}}-0}{\frac{1}{n}}$=$\frac{n+2}{n}$,
故答案为:$\frac{5}{3}$,$\frac{n+2}{n}$.
点评 本题主要考查二次函数图象上点的坐标特征,理解新定义求出所需函数值是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.下列方程中,解是x=2的方程是( )
| A. | 3x+6=0 | B. | $\frac{1}{2}$-$\frac{1}{4}$x=0 | C. | $\frac{2}{3}$x=3 | D. | 5-3x=1 |
15.下列各式中,正确的是( )
| A. | m2•m3=m6 | B. | (2a+b)(a-b)=2a2+ab-b2 | ||
| C. | (5a+2b)(5a-3b)=25a2-6b2 | D. | (x-y)(x2+xy+y2)=x3-y3 |
19.下列计算中,正确的是( )
| A. | a•a=2a | B. | x+x4=x5 | C. | x3•x2=x5 | D. | 2a2•a-1=2a3 |
13.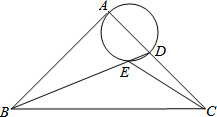 如图,在等腰直角△ABC中,∠BAC=90°,AB=AC,BC=4$\sqrt{2}$,点D是AC上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值是( )
如图,在等腰直角△ABC中,∠BAC=90°,AB=AC,BC=4$\sqrt{2}$,点D是AC上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值是( )
 如图,在等腰直角△ABC中,∠BAC=90°,AB=AC,BC=4$\sqrt{2}$,点D是AC上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值是( )
如图,在等腰直角△ABC中,∠BAC=90°,AB=AC,BC=4$\sqrt{2}$,点D是AC上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值是( )| A. | 2 | B. | 4 | C. | $2\sqrt{2}-2$ | D. | $2\sqrt{5}-2$ |
18.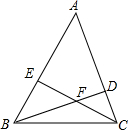 如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为( )
如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为( )
 如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为( )
如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为( )| A. | 20$\sqrt{3}$ | B. | 25$\sqrt{3}$ | C. | 30$\sqrt{3}$ | D. | 40$\sqrt{3}$ |
 如图所示,在每个边长都为1的小正方形组成的网格中,点A、B、C均为格点.
如图所示,在每个边长都为1的小正方形组成的网格中,点A、B、C均为格点. 如图,在正方形ABCD中,△APBC是等边三角形,连接PD,DB,则$\frac{{S}_{△BPD}}{{S}_{正方形ABCD}}$=$\frac{\sqrt{3}-1}{4}$.
如图,在正方形ABCD中,△APBC是等边三角形,连接PD,DB,则$\frac{{S}_{△BPD}}{{S}_{正方形ABCD}}$=$\frac{\sqrt{3}-1}{4}$.