题目内容
9.解方程组(1)$\left\{\begin{array}{l}{x+y=4}\\{2x-y=5}\end{array}\right.$
(2)$\left\{\begin{array}{l}{\frac{x}{2}-\frac{y+1}{3}=1}\\{3x+2y=10}\end{array}\right.$.
分析 (1)方程组中两方程相加消去y求出x的值,进而求出y的值,即可确定出方程组的解;
(2)将两个方程先化简,再选择正确的方法进行消元,本题适合用加减法求解.
解答 解:(1)$\left\{\begin{array}{l}{x+y=4①}\\{2x-y=5②}\end{array}\right.$,
①+②得:3x=9,
解得:x=3,
将x=3代入①得:3+y=4,
解得:y=1,
则原方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$;
(2)化简可得$\left\{\begin{array}{l}{3x-2y=8①}\\{3x+2y=10②}\end{array}\right.$,
①+②,得6x=18,
解得x=3,
①-②,得-4y=-2,
解得y=$\frac{1}{2}$.
∴原方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=\frac{1}{2}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法为:加减消元法与代入消元法.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
14.下列方程中,解是x=2的方程是( )
| A. | 3x+6=0 | B. | $\frac{1}{2}$-$\frac{1}{4}$x=0 | C. | $\frac{2}{3}$x=3 | D. | 5-3x=1 |
19.下列计算中,正确的是( )
| A. | a•a=2a | B. | x+x4=x5 | C. | x3•x2=x5 | D. | 2a2•a-1=2a3 |
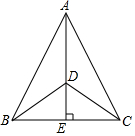 如图,在△ABC中,AB=AC,过点A作AE⊥BC于点E,D为AE上一点,连接DB、DC,∠DBC=α,且$\frac{BD}{AB}$=tanα,记△ABC的面积为S△ABC,△DBC的面积为S△DBC,求$\frac{{S}_{△DBC}}{{S}_{△ABC}}$.
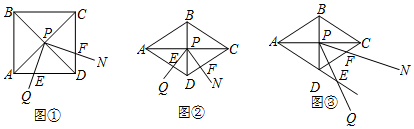
如图,在△ABC中,AB=AC,过点A作AE⊥BC于点E,D为AE上一点,连接DB、DC,∠DBC=α,且$\frac{BD}{AB}$=tanα,记△ABC的面积为S△ABC,△DBC的面积为S△DBC,求$\frac{{S}_{△DBC}}{{S}_{△ABC}}$.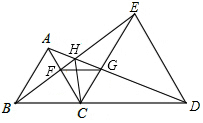 已知,点C是线段BD上一动点,分别以BC、CD为边向同侧作等边△ABC和等边三角形△CDE,如图所示.
已知,点C是线段BD上一动点,分别以BC、CD为边向同侧作等边△ABC和等边三角形△CDE,如图所示.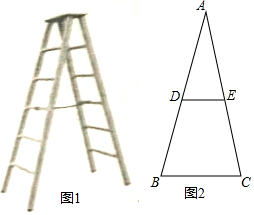 如图1所示的是由梯子AB和梯子AC搭成的“人字梯”,它的5个踩档把梯子等分成6份,梯子的第三踩档处有一条绑绳DE,将其抽象成图2,其中AB=AC=2米.
如图1所示的是由梯子AB和梯子AC搭成的“人字梯”,它的5个踩档把梯子等分成6份,梯子的第三踩档处有一条绑绳DE,将其抽象成图2,其中AB=AC=2米.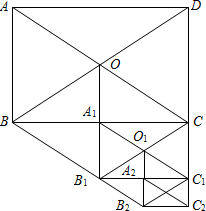 如图所示,在矩形ABCD中,AB=12,AC=20,两条对角线相交于点O.以OB、OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1,再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1、O1C1为邻边作第3个平行四边形O1B1B2C1…依此类推.则第6个平行四边形的面积为( )
如图所示,在矩形ABCD中,AB=12,AC=20,两条对角线相交于点O.以OB、OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1,再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1、O1C1为邻边作第3个平行四边形O1B1B2C1…依此类推.则第6个平行四边形的面积为( )