题目内容
2.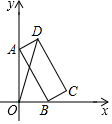 如图,矩形ABCD中,AB=8,BC=3,顶点A,B分别在y轴和x轴上,当点A在y轴上移动时,点B也随之在x轴上移动,在移动过程中,OD的最大值为( )
如图,矩形ABCD中,AB=8,BC=3,顶点A,B分别在y轴和x轴上,当点A在y轴上移动时,点B也随之在x轴上移动,在移动过程中,OD的最大值为( )| A. | 8 | B. | $\sqrt{73}$ | C. | $\sqrt{85}$ | D. | 9 |
分析 取AB的中点E,连接OE、DE、OD,根据三角形的任意两边之和大于第三边可知当O、D、E三点共线时,点D到点O的距离最大,再根据勾股定理求出DE的长,根据直角三角形斜边上的中线等于斜边的一半求出OE的长,两者相加即可得解.
解答 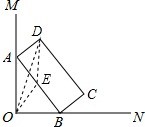 解:如图,取AB的中点E,连接OE、DE,
解:如图,取AB的中点E,连接OE、DE,
∵OD≤OE+DE,
∴当O、D、E三点共线时,点D到点O的距离最大,
此时,∵AB=8,BC=3,
∴OE=AE=$\frac{1}{2}$AB=4,
∴DE=$\sqrt{A{D}^{2}+A{E}^{2}}$=5,
∴OD的最大值为:5+4=9;
故选:D.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半得到性质,三角形的三边关系,矩形的性质,勾股定理,根据三角形的三边关系判断出点O、E、D三点共线时,点D到点O的距离最大是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.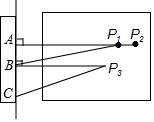 如图是一跳远运动员跳落沙坑时留下的痕迹,则表示该运动员成绩的是( )
如图是一跳远运动员跳落沙坑时留下的痕迹,则表示该运动员成绩的是( )
 如图是一跳远运动员跳落沙坑时留下的痕迹,则表示该运动员成绩的是( )
如图是一跳远运动员跳落沙坑时留下的痕迹,则表示该运动员成绩的是( )| A. | 线段AP1的长 | B. | 线段AP2的长 | C. | 线段BP3的长 | D. | 线段CP3的长 |
14.下列方程中,解是x=2的方程是( )
| A. | 3x+6=0 | B. | $\frac{1}{2}$-$\frac{1}{4}$x=0 | C. | $\frac{2}{3}$x=3 | D. | 5-3x=1 |
11.顺次连接对角线互相垂直的四边形的各边中点,所得图形一定是( )
| A. | 正方形 | B. | 矩形 | C. | 菱形 | D. | 直角梯形 |
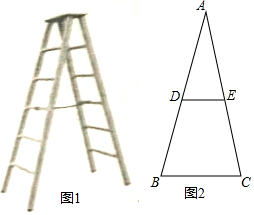 如图1所示的是由梯子AB和梯子AC搭成的“人字梯”,它的5个踩档把梯子等分成6份,梯子的第三踩档处有一条绑绳DE,将其抽象成图2,其中AB=AC=2米.
如图1所示的是由梯子AB和梯子AC搭成的“人字梯”,它的5个踩档把梯子等分成6份,梯子的第三踩档处有一条绑绳DE,将其抽象成图2,其中AB=AC=2米. 如图所示,在每个边长都为1的小正方形组成的网格中,点A、B、C均为格点.
如图所示,在每个边长都为1的小正方形组成的网格中,点A、B、C均为格点.