题目内容
12.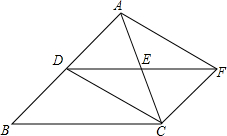 如图,D、E分别是△ABC的边AB、AC上的点,DE=EF,AE=EC,DE∥
如图,D、E分别是△ABC的边AB、AC上的点,DE=EF,AE=EC,DE∥BC,求证:
(1)四边形ADCF是平行四边形;
(2)四边形BCFD是平行四边形.
分析 (1)由对角线互相平分的四边形是平行四边形即可得出结论;
(2)由平行线的性质得出AD=BD,得出DE是△ABC的中位线,由三角形中位线定理得出DE=$\frac{1}{2}$BC,证出BC=DF,即可得出四边形BCFD是平行四边形.
解答 证明:(1)∵DE=EF,AE=EC,
∴四边形ADCF是平行四边形;
(2)∵AE=EC,DE∥BC,
∴AD=BD,
∴DE是△ABC的中位线,
∴DE=$\frac{1}{2}$BC,
∵DE=EF=$\frac{1}{2}$DF,
∴BC=DF,
又∵DF∥BC,
∴四边形BCFD是平行四边形.
点评 本题考查了平行四边形的判定方法、三角形中位线定理;熟记平行四边形的判定方法是解决问题的关键.

练习册系列答案
相关题目
7. 如图所示,∠CAB的外角等于120°,∠B等于40°,则∠C的度数是( )
如图所示,∠CAB的外角等于120°,∠B等于40°,则∠C的度数是( )
 如图所示,∠CAB的外角等于120°,∠B等于40°,则∠C的度数是( )
如图所示,∠CAB的外角等于120°,∠B等于40°,则∠C的度数是( )| A. | 60° | B. | 70° | C. | 80° | D. | 90° |
4.下列说法正确的是( )
| A. | 明天下雨的概率大 | |
| B. | 任意抛掷两颗完全相同的均匀的正四面体骰子,其点数之和为11的概率为零 | |
| C. | 随机说出3个正整数,以这三个数为边长一定能围成一个三角形 | |
| D. | 一副扑克牌,去掉大小王,从中任抽一张,恰好抽到的牌是10的概率为$\frac{1}{13}$ |
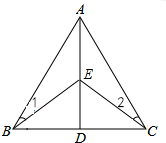 如图,在△ABC中,AD垂直平分BC,点E在AD上,求证:∠1=∠2.
如图,在△ABC中,AD垂直平分BC,点E在AD上,求证:∠1=∠2.