题目内容
1.在△ABC中,∠C=90°,BC=2,AB=6,求∠A的正弦和余弦的值.分析 先由勾股定理得出AC,再根据三角函数的定义得到sinA=$\frac{BC}{AB}$,cosA=$\frac{AC}{AB}$,进行计算即可求解.
解答 解:∵∠C=90°,BC=2,AB=6,
∴AC=4$\sqrt{2}$,
∴sinA=$\frac{BC}{AB}$=$\frac{1}{3}$,
cosA=$\frac{AC}{AB}$=$\frac{2\sqrt{3}}{3}$.
点评 本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
相关题目
13.有下列结论:①sin230°+cos230°=sin260°;②sin45°=cos45°;③tan25°•tan65°=1;④若∠A为锐角,且sinA=cos28°,则∠A=62°.其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.已知m+n-3(m-2n)=P,-5m-4n+(6m-4n)=Q,则m+n的结果( )
| A. | P+Q | B. | -P-Q | C. | P | D. | -Q |
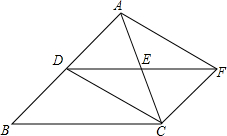 如图,D、E分别是△ABC的边AB、AC上的点,DE=EF,AE=EC,DE∥
如图,D、E分别是△ABC的边AB、AC上的点,DE=EF,AE=EC,DE∥ 如图,AB=AC,∠BAC=120°,AD⊥AC,AE⊥AB.
如图,AB=AC,∠BAC=120°,AD⊥AC,AE⊥AB. 如图,若线段AC=2,AC=$\frac{1}{5}$AB,点D是线段BC的中点,求线段AD的长度.
如图,若线段AC=2,AC=$\frac{1}{5}$AB,点D是线段BC的中点,求线段AD的长度.