题目内容
2.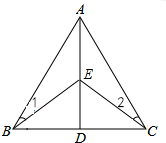 如图,在△ABC中,AD垂直平分BC,点E在AD上,求证:∠1=∠2.
如图,在△ABC中,AD垂直平分BC,点E在AD上,求证:∠1=∠2.
分析 由AD垂直平分BC,得到AB=AC,EB=EC,BD=CD,可证得△ABD≌△ACD,得到∠ABC=∠ACB,同理证得∠EBD=∠ECD,即可得到结论.
解答 证明:∵AD垂直平分BC,
∴AB=AC,EB=EC,BD=CD,
在△ABD和△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{AD=AD}\\{BD=CD}\end{array}\right.$,
∴△ABD≌△ACD,
∴∠ABC=∠ACB,
同理:△DBD≌△ECD,
∴∠EBD=∠ECD,
∴∠1=∠2.
点评 本题主要考查了线段的垂直平分线的性质,全等三角形的判定与性质,解题的关键是熟练掌握全等三角形的判定与性质.

练习册系列答案
相关题目
13.有下列结论:①sin230°+cos230°=sin260°;②sin45°=cos45°;③tan25°•tan65°=1;④若∠A为锐角,且sinA=cos28°,则∠A=62°.其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.已知m+n-3(m-2n)=P,-5m-4n+(6m-4n)=Q,则m+n的结果( )
| A. | P+Q | B. | -P-Q | C. | P | D. | -Q |
10.已知两边及其中一边的对角作三角形,下列结论正确的是( )
| A. | 有唯一一个三角形 | B. | 不能作出三角形 | ||
| C. | 有两个三角形 | D. | 以上三种情况都有可能 |
 如图,D、E分别是△ABC的边AB、AC上的点,DE=EF,AE=EC,DE∥
如图,D、E分别是△ABC的边AB、AC上的点,DE=EF,AE=EC,DE∥ 正方形ABCD中,∠EAF=45°,连接对角线BD交AE于M,交AF于N,求证:以DN、BM、MN为三边的三角形为直角三角形.
正方形ABCD中,∠EAF=45°,连接对角线BD交AE于M,交AF于N,求证:以DN、BM、MN为三边的三角形为直角三角形.
 如图,若线段AC=2,AC=$\frac{1}{5}$AB,点D是线段BC的中点,求线段AD的长度.
如图,若线段AC=2,AC=$\frac{1}{5}$AB,点D是线段BC的中点,求线段AD的长度.