题目内容
11．平面直角坐标系中，点A（-3，2），B（3，4），C（x，y），若AC∥x轴，则线段BC的长度最小时点C的坐标为（ ）| A． | （-3，4） | B． | （3，2） | C． | （3，0） | D． | （4，2） |
分析 由AC∥x轴，可得点C与点A的纵坐标相同，再根据垂线段最短可知BC⊥AC时，BC有最小值，从而可确定点C的坐标．
解答 解：如图所示：
由垂线段最短可知：当BC⊥AC时，BC有最小值．
所以点C的坐标为（3，2），线段的最小值为2．
故选：B．
点评 本题主要考查的是两点间的距离公式、垂线段的性质、点的坐标的定义，掌握垂线段的性质是解题的关键．
练习册系列答案
相关题目
1．在一个口袋中装有1个红球，2个蓝球和1个白球，这些球除颜色外都相同，从中随机摸出两个球，两个球的颜色正好是一红一蓝，则能配成紫色，则摸出的两个球的颜色能配成紫色的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{5}{12}$ |
19．下列条件不能判定△ABC为直角三角形的是（ ）
| A． | ∠A：∠B：∠C=1：2：3 | B． | a：b：c=1：1：$\sqrt{2}$ | C． | a：b：c=3：4：5 | D． | a：b：c=2：2：3 |
6．
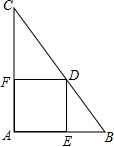如图，在△ABC中，∠A=90°，AC=8，AB=6，点D是BC边上一动点（不与点B、C重合），过点D作DE⊥AB于点E，DF⊥AC于点F，则EF的最小值等于（ ）
如图，在△ABC中，∠A=90°，AC=8，AB=6，点D是BC边上一动点（不与点B、C重合），过点D作DE⊥AB于点E，DF⊥AC于点F，则EF的最小值等于（ ）| A． | $\frac{1}{4}$ | B． | $\frac{24}{5}$ | C． | 5 | D． | $\frac{11}{2}$ |
16．如果$\sqrt{a（a-4）}$=$\sqrt{a}$•$\sqrt{a-4}$，则（ ）
| A． | a≥4 | B． | a≥0 | C． | 0≤a≤4 | D． | a为一切实数 |
20．下列直线是圆的切线的是（ ）
| A． | 与圆有公共点的直线 | B． | 到圆心的距离等于半径的直线 | ||
| C． | 到圆心的距离大于半径的直线 | D． | 到圆心的距离小于半径的直线 |
二次函数y=ax2+bx+c的图象如图，则直线y=ax+bc的图象不经过第三象限．