题目内容
1.在一个口袋中装有1个红球,2个蓝球和1个白球,这些球除颜色外都相同,从中随机摸出两个球,两个球的颜色正好是一红一蓝,则能配成紫色,则摸出的两个球的颜色能配成紫色的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{12}$ |
分析 根据题意画出树状图,列举出所有的可能,进而得出答案.
解答 解:如图所示: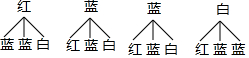 ,
,
一共有12种可能,正好是一红一蓝一共有4个,
故摸出的两个球的颜色能配成紫色的概率是:$\frac{4}{12}$=$\frac{1}{3}$.
故选:B.
点评 此题主要考查了树状图法求概率,正确画出树状图是解题关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
11.若一个数的绝对值的相反数是-$\frac{1}{7}$,则这个数是( )
| A. | -$\frac{1}{7}$ | B. | +$\frac{1}{7}$ | C. | ±$\frac{1}{7}$ | D. | ±7 |
12. 有理数a,b在数轴上对应的位置如图,则( )
有理数a,b在数轴上对应的位置如图,则( )
 有理数a,b在数轴上对应的位置如图,则( )
有理数a,b在数轴上对应的位置如图,则( )| A. | a+b<0 | B. | a+b>0 | C. | a-b=0 | D. | a-b>0 |
9.下列说法中正确的有( )个
①两数的和一定大于每一个加数;
②两数的积一定大于每一个因数;
③几个有理数的和是正数,则至少有一个加数是正数;
④几个有理数的积是正数,则至少有一个因数是正数;
⑤几个有理数的积是0,则至少有一个因数是0.
①两数的和一定大于每一个加数;
②两数的积一定大于每一个因数;
③几个有理数的和是正数,则至少有一个加数是正数;
④几个有理数的积是正数,则至少有一个因数是正数;
⑤几个有理数的积是0,则至少有一个因数是0.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 1个 |
16.在数轴上与表示-2的点相距5个单位长度的点所表示的数是( )
| A. | 3 | B. | -7 | C. | 7 | D. | 3或-7 |
6.下列运算正确的是( )
| A. | a+a2=a3 | B. | a2•a3=a6 | C. | a5÷a3=a2 | D. | (a2)3=a5 |
13.在等式3-[3(x+2y)-3(_______)]=-6x-6y中,括号内填入的代数式应是( )
| A. | -x+1 | B. | -x-1 | C. | x+1 | D. | -x-1 |
10.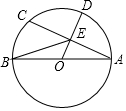 如图,AB是⊙O的直径,AB=10,弦AC=8,OD⊥AC于E,交⊙O于D,连接BE,则BE的长为( )
如图,AB是⊙O的直径,AB=10,弦AC=8,OD⊥AC于E,交⊙O于D,连接BE,则BE的长为( )
 如图,AB是⊙O的直径,AB=10,弦AC=8,OD⊥AC于E,交⊙O于D,连接BE,则BE的长为( )
如图,AB是⊙O的直径,AB=10,弦AC=8,OD⊥AC于E,交⊙O于D,连接BE,则BE的长为( )| A. | $\sqrt{13}$ | B. | 2$\sqrt{13}$ | C. | 5 | D. | 6 |
11.平面直角坐标系中,点A(-3,2),B(3,4),C(x,y),若AC∥x轴,则线段BC的长度最小时点C的坐标为( )
| A. | (-3,4) | B. | (3,2) | C. | (3,0) | D. | (4,2) |