题目内容
19.下列条件不能判定△ABC为直角三角形的是( )| A. | ∠A:∠B:∠C=1:2:3 | B. | a:b:c=1:1:$\sqrt{2}$ | C. | a:b:c=3:4:5 | D. | a:b:c=2:2:3 |
分析 由三角形内角和定理及勾股定理的逆定理进行判断即可.
解答 解:A、∵∠A:∠B:∠C=1:2:3,∴∠C=$\frac{3}{6}$×180°=90°,故能判定△ABC为直角三角形;
B、设a=k,b=k,c=$\sqrt{2}$k,k2+k2=($\sqrt{2}$k)2,故能判定△ABC为直角三角形;
C、设a=3k,b=4k,c=5k,(3k)2+(4k)2=(5k)2,故能判定△ABC为直角三角形;
D、设a=2k,b=2k,c=3k,(2k)2+(2k)2≠(3k)2,故不能判定△ABC为直角三角形.
故选D.
点评 本题考查了直角三角形的判定,注意在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.

练习册系列答案
相关题目
9.下列说法中正确的有( )个
①两数的和一定大于每一个加数;
②两数的积一定大于每一个因数;
③几个有理数的和是正数,则至少有一个加数是正数;
④几个有理数的积是正数,则至少有一个因数是正数;
⑤几个有理数的积是0,则至少有一个因数是0.
①两数的和一定大于每一个加数;
②两数的积一定大于每一个因数;
③几个有理数的和是正数,则至少有一个加数是正数;
④几个有理数的积是正数,则至少有一个因数是正数;
⑤几个有理数的积是0,则至少有一个因数是0.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 1个 |
10.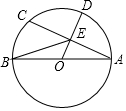 如图,AB是⊙O的直径,AB=10,弦AC=8,OD⊥AC于E,交⊙O于D,连接BE,则BE的长为( )
如图,AB是⊙O的直径,AB=10,弦AC=8,OD⊥AC于E,交⊙O于D,连接BE,则BE的长为( )
 如图,AB是⊙O的直径,AB=10,弦AC=8,OD⊥AC于E,交⊙O于D,连接BE,则BE的长为( )
如图,AB是⊙O的直径,AB=10,弦AC=8,OD⊥AC于E,交⊙O于D,连接BE,则BE的长为( )| A. | $\sqrt{13}$ | B. | 2$\sqrt{13}$ | C. | 5 | D. | 6 |
4.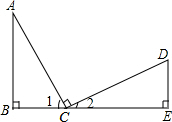 已知:如图所示,BC=ED,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
已知:如图所示,BC=ED,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
 已知:如图所示,BC=ED,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
已知:如图所示,BC=ED,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )| A. | ∠A与∠D互为余角 | B. | ∠A=∠2 | C. | △ABC≌△CED | D. | AB=CD |
11.平面直角坐标系中,点A(-3,2),B(3,4),C(x,y),若AC∥x轴,则线段BC的长度最小时点C的坐标为( )
| A. | (-3,4) | B. | (3,2) | C. | (3,0) | D. | (4,2) |
8.若分式$\frac{{x}^{2}-1}{x-1}$的值为0,则x取值为( )
| A. | x=1 | B. | x=-1 | C. | x=0 | D. | x=±1 |
 如图,在△ABC中,∠ABC=90°,D是AC上一点,AD=AB.若∠A=50°,则∠DBC=25°.
如图,在△ABC中,∠ABC=90°,D是AC上一点,AD=AB.若∠A=50°,则∠DBC=25°. 如图,在△ABC中,D是BC边上的中点,∠BDE=∠CDE,请你添加一个条件,使DE=DF,你添加的条件是∠B=∠C或∠BED=∠CFD(不再添加辅助线和字母)
如图,在△ABC中,D是BC边上的中点,∠BDE=∠CDE,请你添加一个条件,使DE=DF,你添加的条件是∠B=∠C或∠BED=∠CFD(不再添加辅助线和字母)