题目内容
6.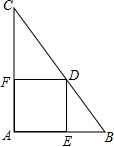 如图,在△ABC中,∠A=90°,AC=8,AB=6,点D是BC边上一动点(不与点B、C重合),过点D作DE⊥AB于点E,DF⊥AC于点F,则EF的最小值等于( )
如图,在△ABC中,∠A=90°,AC=8,AB=6,点D是BC边上一动点(不与点B、C重合),过点D作DE⊥AB于点E,DF⊥AC于点F,则EF的最小值等于( )| A. | $\frac{1}{4}$ | B. | $\frac{24}{5}$ | C. | 5 | D. | $\frac{11}{2}$ |
分析 连接CD,利用勾股定理列式求出AB,判断出四边形CFDE是矩形,根据矩形的对角线相等可得EF=CD,再根据垂线段最短可得CD⊥AB时,线段EF的值最小,然后根据三角形的面积公式列出方程求解即可.
解答 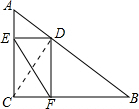 解:如图,连接CD.
解:如图,连接CD.
∵∠ACB=90°,AC=6,BC=8,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=10,
∵PE⊥AC,PF⊥BC,∠C=90°,
∴四边形CFDE是矩形,
∴EF=CD,
由垂线段最短可得CD⊥AB时,线段EF的值最小,
此时,S△ABC=$\frac{1}{2}$BC•AC=$\frac{1}{2}$AB•CD,
即$\frac{1}{2}$×8×6=$\frac{1}{2}$×10•CD,
解得CD=4.8,
∴EF=4.8.
故选B.
点评 本题考查了矩形的判定与性质,垂线段最短的性质,勾股定理,判断出CD⊥AB时,线段EF的值最小是解题的关键,难点在于利用三角形的面积列出方程.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
16.在数轴上与表示-2的点相距5个单位长度的点所表示的数是( )
| A. | 3 | B. | -7 | C. | 7 | D. | 3或-7 |
17.多项式axy2-$\frac{1}{3}$x与bxy2+$\frac{3}{4}$x的和是一个单项式,则a,b的关系是 ( )
| A. | a=-b | B. | a=b=0 | C. | a=b | D. | 不能确定 |
11.平面直角坐标系中,点A(-3,2),B(3,4),C(x,y),若AC∥x轴,则线段BC的长度最小时点C的坐标为( )
| A. | (-3,4) | B. | (3,2) | C. | (3,0) | D. | (4,2) |
18.下列等式或说法一定正确的是( )
| A. | $\sqrt{\frac{a}{b}}$=$\frac{\sqrt{a}}{\sqrt{b}}$ | B. | $\sqrt{{a}^{2}-{b}^{2}}$不是最简根式 | ||
| C. | 若a<0,则$\sqrt{{a}^{4}}$=a2 | D. | $\sqrt{18}$或$\sqrt{48}$是同类二次根式 |
15. 如图,在由六个全等的正三角形拼成的图中,菱形的个数为( )
如图,在由六个全等的正三角形拼成的图中,菱形的个数为( )
 如图,在由六个全等的正三角形拼成的图中,菱形的个数为( )
如图,在由六个全等的正三角形拼成的图中,菱形的个数为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
 如图,在△ABC中,D是BC边上的中点,∠BDE=∠CDE,请你添加一个条件,使DE=DF,你添加的条件是∠B=∠C或∠BED=∠CFD(不再添加辅助线和字母)
如图,在△ABC中,D是BC边上的中点,∠BDE=∠CDE,请你添加一个条件,使DE=DF,你添加的条件是∠B=∠C或∠BED=∠CFD(不再添加辅助线和字母)