题目内容
1．
二次函数y=ax2+bx+c的图象如图，则直线y=ax+bc的图象不经过第三象限．
分析 先由二次函数的图象确定a、b、c字母系数的正负，再求出一次函数的图象所过的象限即可．
解答 解：由图象可知抛物线开口向下，
∴a＜0，
∵对称轴在y轴右侧，
∴对称轴x=-$\frac{b}{2a}$＞0，
∴b＞0；
∵抛物线与y轴的交点为在y轴的正半轴上，
∴c＞0；
∵b＞0，c＞0
∴一次函数y=ax+bc的图象不经过第三象限．
故答案为三．
点评 本题考查了二次函数的图象与系数的关系，根据二次函数的图象确定二次函数的字母系数的取值范围是解题的关键．
练习册系列答案
相关题目
11．平面直角坐标系中，点A（-3，2），B（3，4），C（x，y），若AC∥x轴，则线段BC的长度最小时点C的坐标为（ ）
| A． | （-3，4） | B． | （3，2） | C． | （3，0） | D． | （4，2） |
13．顶点为（5，1），形状与函数y=$\frac{1}{3}$x2的图象相同且开口方向相反的抛物线是（ ）
| A． | y=-$\frac{1}{3}{（{x-5}）^2}$+1 | B． | y=-$\frac{1}{3}$x2-5 | C． | y=-$\frac{1}{3}$（x-5）2-1 | D． | y=$\frac{1}{3}$（x+5）2-1 |
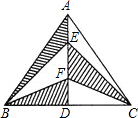如图，在△ABC中，AB=AC，点D是BC中点，若BC=5，AD=4，则图中阴影部分的面积为5．