题目内容
10.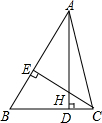 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于一点H,已知EH=EB=9,AE=12,则CH的长是( )
如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于一点H,已知EH=EB=9,AE=12,则CH的长是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 本题可先根据AAS判定△AEH≌△CEB,可得出AE=CE,从而得出CH=CE-EH=12-9=3.
解答 解:在△ABC中,AD⊥BC,CE⊥AB,
∴∠AEH=∠ADB=90°;
∵∠EAH+∠AHE=90°,∠DHC+∠BCH=90°,
∵∠EHA=∠DHC(对顶角相等),
∴∠EAH=∠DCH(等量代换);
∵在△BCE和△HAE中
$\left\{\begin{array}{l}{∠BEC=∠HEA}\\{∠BCE=∠HAE}\\{BE=HE}\end{array}\right.$,
∴△AEH≌△CEB(AAS);
∴AE=CE;
∵EH=EB=9,AE=12,
∴CH=CE-EH=AE-EH=12-9=3,
故选C
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA,AAS、HL,要熟练掌握并灵活应用这些方法.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
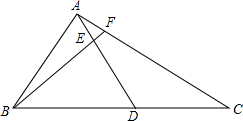 △ABC中,D为BC上的一点,$\frac{BD}{DC}=2$,E是AD上一点,$\frac{AE}{ED}=\frac{1}{4}$,求$\frac{BE}{EF}$,$\frac{AF}{FC}$的值.
△ABC中,D为BC上的一点,$\frac{BD}{DC}=2$,E是AD上一点,$\frac{AE}{ED}=\frac{1}{4}$,求$\frac{BE}{EF}$,$\frac{AF}{FC}$的值.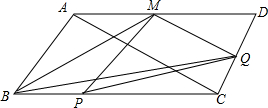 已知,如图,平行四边形ABCD中,AB=6cm,BC=10cm,∠BAC=90°,点P在线段BC上由B向C匀速运动,速度为2cm/s,点Q在线段CD上,由C向D匀速运动,速度是1cm/s.(P、Q两个点同时出发)连接PQ,设运动时间为t(s),(0<t<4).过点Q做MQ∥AC交AD与M.
已知,如图,平行四边形ABCD中,AB=6cm,BC=10cm,∠BAC=90°,点P在线段BC上由B向C匀速运动,速度为2cm/s,点Q在线段CD上,由C向D匀速运动,速度是1cm/s.(P、Q两个点同时出发)连接PQ,设运动时间为t(s),(0<t<4).过点Q做MQ∥AC交AD与M. 已知:如图,AB=DE,BC=EF,∠B=∠E,求证:AC∥DF.
已知:如图,AB=DE,BC=EF,∠B=∠E,求证:AC∥DF.
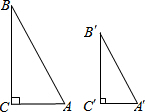 学习(图形的相似)后,我们可以借助探索两个直角三角形全等的条件所获得的经验,继续探索两个直角三角形相似的条件,“满足斜边和一条直角边对应相等的两个直角三角形全等”,类似地,你可以得到:“满足斜边和一条直角边的比相等的两个直角三角形相似”,请结合下列所给图形,写出已知、求证,并完成说理过程.
学习(图形的相似)后,我们可以借助探索两个直角三角形全等的条件所获得的经验,继续探索两个直角三角形相似的条件,“满足斜边和一条直角边对应相等的两个直角三角形全等”,类似地,你可以得到:“满足斜边和一条直角边的比相等的两个直角三角形相似”,请结合下列所给图形,写出已知、求证,并完成说理过程.