题目内容
14.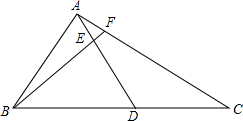 △ABC中,D为BC上的一点,$\frac{BD}{DC}=2$,E是AD上一点,$\frac{AE}{ED}=\frac{1}{4}$,求$\frac{BE}{EF}$,$\frac{AF}{FC}$的值.
△ABC中,D为BC上的一点,$\frac{BD}{DC}=2$,E是AD上一点,$\frac{AE}{ED}=\frac{1}{4}$,求$\frac{BE}{EF}$,$\frac{AF}{FC}$的值.
分析 作DG∥AC交BF于G,如图,根据平行线分线段成比例定理,由DG∥CF得$\frac{BG}{BF}$=$\frac{DG}{CF}=\frac{BD}{BC}$=$\frac{2}{3}$,FC=$\frac{3}{2}$DG,GF=$\frac{1}{3}$BF,由DG∥AF,于是得到$\frac{EF}{GE}$=$\frac{AF}{DG}=\frac{AE}{ED}$=$\frac{1}{4}$,AF=$\frac{1}{4}$DG,EF=$\frac{1}{4}$EG,即可得到结论.
解答 解: 作DG∥AC交BF于G,如图,
作DG∥AC交BF于G,如图,
∵$\frac{BD}{DC}=2$,
∴$\frac{BD}{BC}$=$\frac{2}{3}$,
∵DG∥CF,
∴$\frac{BG}{BF}$=$\frac{DG}{CF}=\frac{BD}{BC}$=$\frac{2}{3}$,
∴FC=$\frac{3}{2}$DG,GF=$\frac{1}{3}$BF,
∵DG∥AF,
∴$\frac{EF}{GE}$=$\frac{AF}{DG}=\frac{AE}{ED}$=$\frac{1}{4}$,
∴AF=$\frac{1}{4}$DG,EF=$\frac{1}{4}$EG,
∴AF:FC=$\frac{1}{6}$,$\frac{BE}{EF}$=14:1.
点评 本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例;平行于三角形的一边,并且和其他两边(或两边的延长线)相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.也考查了比例的性质.

练习册系列答案
相关题目
9.已知x>y>0,则$\frac{y+1}{x+1}$-$\frac{y}{x}$的值为( )
| A. | 正数 | B. | 负数 | C. | 零 | D. | 无法确定 |
 如图,张大爷有一块三角形土地ABC,测得AC=6,BC=12,AB=10,原有一条机耕路AD,且AD⊥BC,现在张大爷想把这条机耕路挖掉,请计算这条机耕路的长度.
如图,张大爷有一块三角形土地ABC,测得AC=6,BC=12,AB=10,原有一条机耕路AD,且AD⊥BC,现在张大爷想把这条机耕路挖掉,请计算这条机耕路的长度. 如图,分别写出菱形ABCD的4个顶点的坐标:A(0,-1),B(2,2),C(0,5),D(-2,2).
如图,分别写出菱形ABCD的4个顶点的坐标:A(0,-1),B(2,2),C(0,5),D(-2,2).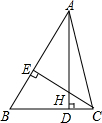 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于一点H,已知EH=EB=9,AE=12,则CH的长是( )
如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于一点H,已知EH=EB=9,AE=12,则CH的长是( )