题目内容
20.已知|2a+1|+(4b-2)2=0,求:(-$\frac{3}{2}$a+$\frac{1}{3}$b2)-(a-$\frac{1}{3}$b2)-($\frac{1}{2}a$+b)的值.分析 先由非负数的性质求得a、b的值,然后化简多项式,最后代入数值进行计算即可.
解答 解:∵|2a+1|+(4b-2)2=0,
∴a=-$\frac{1}{2}$,b=$\frac{1}{2}$.
(-$\frac{3}{2}$a+$\frac{1}{3}$b2)-(a-$\frac{1}{3}$b2)-($\frac{1}{2}a$+b)
=-$\frac{3}{2}$a+$\frac{1}{3}$b2-a+$\frac{1}{3}$b2-$\frac{1}{2}a$-b
=$\frac{2}{3}{b}^{2}-3a-b$
当a=-$\frac{1}{2}$,b=$\frac{1}{2}$时,原式=$\frac{2}{3}×\frac{1}{4}-3×(-\frac{1}{2})-\frac{1}{2}$=$\frac{7}{6}$.
点评 本题主要考查的是非负数的性质、整式的加减,利用非负数的性质求得a、b的值是解题的关键.

练习册系列答案
相关题目
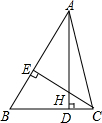 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于一点H,已知EH=EB=9,AE=12,则CH的长是( )
如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于一点H,已知EH=EB=9,AE=12,则CH的长是( ) 如图,AD、BC是⊙O的两条互相垂直的直径,点P从O点出发,沿0CDO的路线匀速运动,设点P运动的时间为x(单位:秒),∠APB=y(单位:度),那么表示y与x之间关系的图象是( )
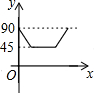
如图,AD、BC是⊙O的两条互相垂直的直径,点P从O点出发,沿0CDO的路线匀速运动,设点P运动的时间为x(单位:秒),∠APB=y(单位:度),那么表示y与x之间关系的图象是( )


 如图,△ABC是等边三角形,∠CBD=90°,BD=BC,则∠1的度数是75°.
如图,△ABC是等边三角形,∠CBD=90°,BD=BC,则∠1的度数是75°.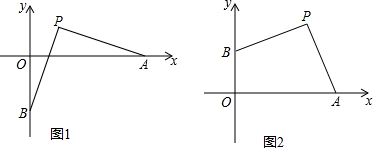
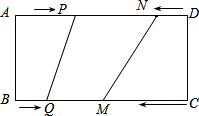 如图,在矩形ABCD中,BC=20cm,P,Q,M,N分别从A,B,C,D出发沿AD,BC,CB,DA方向在矩形的边上同时运动,当有一个点到达所在运动的另一个端点时,运动即停止.已知在相同时间内,若BQ=xcm(x>0),则AP=2xcm,CM=3xcm,DN=x2cm.当x为何值时,以P、Q、M、N为顶点的四边形是平行四边形.
如图,在矩形ABCD中,BC=20cm,P,Q,M,N分别从A,B,C,D出发沿AD,BC,CB,DA方向在矩形的边上同时运动,当有一个点到达所在运动的另一个端点时,运动即停止.已知在相同时间内,若BQ=xcm(x>0),则AP=2xcm,CM=3xcm,DN=x2cm.当x为何值时,以P、Q、M、N为顶点的四边形是平行四边形.