题目内容
19.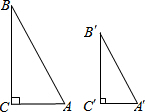 学习(图形的相似)后,我们可以借助探索两个直角三角形全等的条件所获得的经验,继续探索两个直角三角形相似的条件,“满足斜边和一条直角边对应相等的两个直角三角形全等”,类似地,你可以得到:“满足斜边和一条直角边的比相等的两个直角三角形相似”,请结合下列所给图形,写出已知、求证,并完成说理过程.
学习(图形的相似)后,我们可以借助探索两个直角三角形全等的条件所获得的经验,继续探索两个直角三角形相似的条件,“满足斜边和一条直角边对应相等的两个直角三角形全等”,类似地,你可以得到:“满足斜边和一条直角边的比相等的两个直角三角形相似”,请结合下列所给图形,写出已知、求证,并完成说理过程.
分析 类似有斜边和一条直角边的比相等的两个直角三角形相似.写出已知和求证,设$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$=k,则AB=kA′B′,AC=kA′C′,利用勾股定理得到$\frac{BC}{B′C′}$=k,则$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$=$\frac{BC}{B′C′}$,然后根据三组对应边的比相等的两个三角形相似可判断△ABC∽△A′B′C′.
解答 解:求证:斜边和一条直角边的比相等的两个直角三角形相似.
已知:在△ABC和△A′B′C′中,∠C=∠C′=90°,$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$,
求证:△ABC∽△A′B′C′.
证明:设$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$=k,则AB=kA′B′,AC=kA′C′,
在Rt△ABC中,BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{(kA′B′)^{2}-(kA′C′)^{2}}$=k$\sqrt{A′B{′}^{2}-A′C{′}^{2}}$,
在Rt△A′B′C′中,B′C′=$\sqrt{A′B{′}^{2}-A′C{′}^{2}}$,
则$\frac{BC}{B′C′}$=k,
所以$\frac{AB}{A′B′}$=$\frac{AC}{A′C′}$=$\frac{BC}{B′C′}$,
所以△ABC∽△A′B′C′.
即斜边和一条直角边的比相等的两个直角三角形相似.
故答案为斜边和一条直角边的比相等.
点评 本题考查了相似三角形的判定:三组对应边的比相等的两个三角形相似;两组对应边的比相等且夹角对应相等的两个三角形相似.也考查了勾股定理.

 如图,分别写出菱形ABCD的4个顶点的坐标:A(0,-1),B(2,2),C(0,5),D(-2,2).
如图,分别写出菱形ABCD的4个顶点的坐标:A(0,-1),B(2,2),C(0,5),D(-2,2).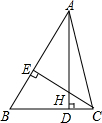 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于一点H,已知EH=EB=9,AE=12,则CH的长是( )
如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD,CE交于一点H,已知EH=EB=9,AE=12,则CH的长是( )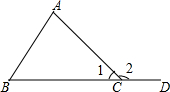 已知,如图,∠2是△ABC的一个外角,求证:∠2=∠A+∠B.
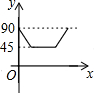
已知,如图,∠2是△ABC的一个外角,求证:∠2=∠A+∠B.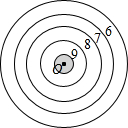 如图所示,小明在劳动课上做了一个靶子,靶心圆的半径为2cm,击中为10环(阴影部分),向外依次是9,8,7,6环,10,9,8,7,6圆环间距离都是3cm.
如图所示,小明在劳动课上做了一个靶子,靶心圆的半径为2cm,击中为10环(阴影部分),向外依次是9,8,7,6环,10,9,8,7,6圆环间距离都是3cm.
 如图,AD、BC是⊙O的两条互相垂直的直径,点P从O点出发,沿0CDO的路线匀速运动,设点P运动的时间为x(单位:秒),∠APB=y(单位:度),那么表示y与x之间关系的图象是( )
如图,AD、BC是⊙O的两条互相垂直的直径,点P从O点出发,沿0CDO的路线匀速运动,设点P运动的时间为x(单位:秒),∠APB=y(单位:度),那么表示y与x之间关系的图象是( )


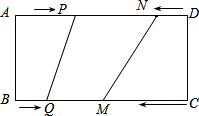 如图,在矩形ABCD中,BC=20cm,P,Q,M,N分别从A,B,C,D出发沿AD,BC,CB,DA方向在矩形的边上同时运动,当有一个点到达所在运动的另一个端点时,运动即停止.已知在相同时间内,若BQ=xcm(x>0),则AP=2xcm,CM=3xcm,DN=x2cm.当x为何值时,以P、Q、M、N为顶点的四边形是平行四边形.
如图,在矩形ABCD中,BC=20cm,P,Q,M,N分别从A,B,C,D出发沿AD,BC,CB,DA方向在矩形的边上同时运动,当有一个点到达所在运动的另一个端点时,运动即停止.已知在相同时间内,若BQ=xcm(x>0),则AP=2xcm,CM=3xcm,DN=x2cm.当x为何值时,以P、Q、M、N为顶点的四边形是平行四边形.