题目内容
如图，已知点P在锐角∠AOB内部，∠AOB=α，在OB边上存在一点D，在OA边上存在一点C，能使PD+DC最小，此时∠PDC=考点：轴对称-最短路线问题
专题：
分析：过P的作关于OB的对称点P'，作P′C⊥OA于C，交OB于D，此时PD+DC=P'C最短，即可求得∠PDC的度数．
解答：解：过P的作关于OB的对称点P'，作P′C⊥OA于C，交OB于D，此时PD=PD′，根据点到直线的距离最短可知PD+DC=P′C最短，
∵∠PDB=∠P′DB，∠CDO=∠P′DB，
∴∠CDO=∠PDB，
∵P′C⊥OA，∠AOB=α，
∴∠CDO=90°-α，
∴∠PDC=180°-2（90°-α）=2α．
故答案为：2α．
∵∠PDB=∠P′DB，∠CDO=∠P′DB，
∴∠CDO=∠PDB，
∵P′C⊥OA，∠AOB=α，
∴∠CDO=90°-α，
∴∠PDC=180°-2（90°-α）=2α．
故答案为：2α．
点评：本题考查了轴对称-最短路线问题的应用、点到直线的距离最短，关键是确定D、C的位置．
练习册系列答案
发散思维新课堂系列答案
相关题目
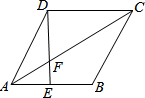如图，?ABCD中，AE：EB=2：3，DE交AC于F．
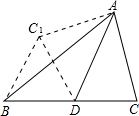如图，AD是△ABC的中线，∠ADC=60°，△ADC沿直线AD解析，点C落在点C1的位置，如果DC=2，那么BC1的值为（ ）
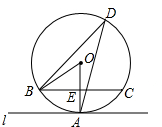如图，直线l与半径为1的⊙O相切于点A，弦BC∥l，D为圆上一点，∠ADB=30°，连接OB、OA，OA交BC于点E．
如图，直线AB，CD相交于点O，过点O画射线OE，若OB平分∠DOE，∠2：∠3=2：5，求∠AOD与∠AOC的度数．
“汶川”地震后，成都乙粮库以每天相同的速度将粮食运往灾区，为缓解成都乙粮库的压力，河南省甲粮库以汽车运输的方式予以支援，如图是两粮库的储粮量y（万吨）与时间x（天）之间的函数图象，在单位时间内甲粮库的出粮量与乙粮库的进粮量是相同的（不考虑粮食的损耗），通过图象回答下列问题．
在同一平面直角坐标系中有3个点：A（2，3），B（-8，3），C（-8，-2）．