题目内容
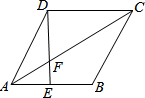 如图,?ABCD中,AE:EB=2:3,DE交AC于F.
如图,?ABCD中,AE:EB=2:3,DE交AC于F.(1)求证:△AEF∽△CDF;
(2)求△AEF与△CDF周长之比;
(3)如果△CDF的面积为20cm2,求△AEF的面积.
考点:相似三角形的判定与性质,平行四边形的性质
专题:
分析:(1)证明DC∥AB,即可解决问题.
(2)运用相似三角形的性质:周长之比等于相似比即可解决问题.
(3)运用相似三角形的性质:面积之比等于相似比的平方即可解决问题.
(2)运用相似三角形的性质:周长之比等于相似比即可解决问题.
(3)运用相似三角形的性质:面积之比等于相似比的平方即可解决问题.
解答: 解:(1)∵四边形ABCD是平行四边形,
解:(1)∵四边形ABCD是平行四边形,
∴DC∥AB,
∴△AEF∽△CDF.
(2)∵四边形ABCD是平行四边形,
∴DC=AB;而AE:EB=2:3,
设AE=2λ,则BE=3λ,DC=5λ;
∵△AEF∽△CDF,
∴
=
=
,
∴△AEF与△CDF周长之比为2:5.
(3)∵△AEF∽△CDF,
∴
=(
)2,而
=
=
,△CDF的面积为20cm2,
∴△AEF的面积为
cm2.
 解:(1)∵四边形ABCD是平行四边形,
解:(1)∵四边形ABCD是平行四边形,∴DC∥AB,
∴△AEF∽△CDF.
(2)∵四边形ABCD是平行四边形,
∴DC=AB;而AE:EB=2:3,
设AE=2λ,则BE=3λ,DC=5λ;
∵△AEF∽△CDF,
∴
| △AEF的周长 |
| △CDF的周长 |
| AE |
| DC |
| 2λ |
| 5λ |
∴△AEF与△CDF周长之比为2:5.
(3)∵△AEF∽△CDF,
∴
| S△CDF |
| S△AEF |
| CD |
| AE |
| CD |
| AE |
| 5λ |
| 2λ |
| 5 |
| 2 |
∴△AEF的面积为
| 16 |
| 5 |
点评:该题以平行四边形为载体,以考查相似三角形的判定及其性质为核心构造而成;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
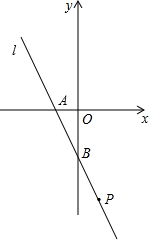 如图,已知,直线l分别交x轴y轴于A、B两点,OA、OB的长满足
如图,已知,直线l分别交x轴y轴于A、B两点,OA、OB的长满足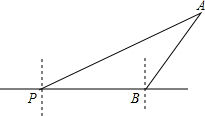 如图,一艘轮船位于P时测得灯塔A在其北偏东60°方向,它沿着正东方向行驶400海里到达B处,此时测得灯塔A在其北偏东30°方向,已知以灯塔A为圆心,300海里为半径的范围内有暗礁存在,请通过计算回答,轮船继续向东航行,是否有触礁的危险.
如图,一艘轮船位于P时测得灯塔A在其北偏东60°方向,它沿着正东方向行驶400海里到达B处,此时测得灯塔A在其北偏东30°方向,已知以灯塔A为圆心,300海里为半径的范围内有暗礁存在,请通过计算回答,轮船继续向东航行,是否有触礁的危险.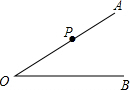 如图,已知∠AOB,P是射线OA上一点,按下列要求作图(保留作图痕迹,不要求写作法)
如图,已知∠AOB,P是射线OA上一点,按下列要求作图(保留作图痕迹,不要求写作法) 如图,已知点P在锐角∠AOB内部,∠AOB=α,在OB边上存在一点D,在OA边上存在一点C,能使PD+DC最小,此时∠PDC=
如图,已知点P在锐角∠AOB内部,∠AOB=α,在OB边上存在一点D,在OA边上存在一点C,能使PD+DC最小,此时∠PDC=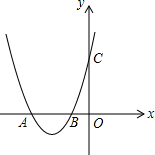 已知:如图,抛物线C1:y=ax2+4ax+c的图象开口向上,与x轴交于点A、B(A在B的左边),与y轴交于点C,顶点为P,AB=2,且OA=OC.
已知:如图,抛物线C1:y=ax2+4ax+c的图象开口向上,与x轴交于点A、B(A在B的左边),与y轴交于点C,顶点为P,AB=2,且OA=OC.