题目内容
 如图,直线AB,CD相交于点O,过点O画射线OE,若OB平分∠DOE,∠2:∠3=2:5,求∠AOD与∠AOC的度数.
如图,直线AB,CD相交于点O,过点O画射线OE,若OB平分∠DOE,∠2:∠3=2:5,求∠AOD与∠AOC的度数.考点:对顶角、邻补角,角平分线的定义
专题:
分析:由OB平分∠DOE,可得:∠1=∠2,由∠2:∠3=2:5,可得:∠1:∠2:∠3=2:2:5,然后由平角的定义可求∠1的度数,最后根据邻补角的定义及对顶角相等即可求出∠AOD与∠AOC的度数.
解答:解:∵OB平分∠DOE,
∴∠1=∠2,
∵∠2:∠3=2:5,
∴∠1:∠2:∠3=2:2:5,
设∠1=2x,∠2=2x,∠3=5x,
∵∠1+∠2+∠3=180°,
∴2x+2x+5x=180°,
解得:x=20°,
∴∠1=2x=40°,∠2=2x=40°,∠3=5x=100°,
∵∠AOD+∠1=180°,
∴∠AOD=140°,
∵∠AOC与∠1是对顶角,
∴∠AOC=∠1=40°.
∴∠AOD=140°,∠AOC=40°.
∴∠1=∠2,
∵∠2:∠3=2:5,
∴∠1:∠2:∠3=2:2:5,
设∠1=2x,∠2=2x,∠3=5x,
∵∠1+∠2+∠3=180°,
∴2x+2x+5x=180°,
解得:x=20°,
∴∠1=2x=40°,∠2=2x=40°,∠3=5x=100°,
∵∠AOD+∠1=180°,
∴∠AOD=140°,
∵∠AOC与∠1是对顶角,
∴∠AOC=∠1=40°.
∴∠AOD=140°,∠AOC=40°.
点评:此题考查了邻补角的定义及对顶角的性质,解题的关键是:根据角平分线的性质及平角的定义求出∠1的度数.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
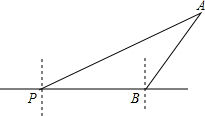 如图,一艘轮船位于P时测得灯塔A在其北偏东60°方向,它沿着正东方向行驶400海里到达B处,此时测得灯塔A在其北偏东30°方向,已知以灯塔A为圆心,300海里为半径的范围内有暗礁存在,请通过计算回答,轮船继续向东航行,是否有触礁的危险.
如图,一艘轮船位于P时测得灯塔A在其北偏东60°方向,它沿着正东方向行驶400海里到达B处,此时测得灯塔A在其北偏东30°方向,已知以灯塔A为圆心,300海里为半径的范围内有暗礁存在,请通过计算回答,轮船继续向东航行,是否有触礁的危险. 如图,已知点P在锐角∠AOB内部,∠AOB=α,在OB边上存在一点D,在OA边上存在一点C,能使PD+DC最小,此时∠PDC=
如图,已知点P在锐角∠AOB内部,∠AOB=α,在OB边上存在一点D,在OA边上存在一点C,能使PD+DC最小,此时∠PDC= 如图所示,已知等边三角形ABC的两个顶点坐标为A(-4,0),B(2,0),CH⊥AB,试求点C的坐标和△ABC的面积.
如图所示,已知等边三角形ABC的两个顶点坐标为A(-4,0),B(2,0),CH⊥AB,试求点C的坐标和△ABC的面积. 直线y=
直线y=
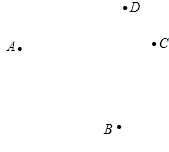 已知平面上A、B、C、D四个点,按下列要求画出图形:
已知平面上A、B、C、D四个点,按下列要求画出图形: