题目内容
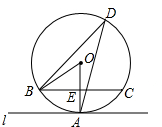 如图,直线l与半径为1的⊙O相切于点A,弦BC∥l,D为圆上一点,∠ADB=30°,连接OB、OA,OA交BC于点E.
如图,直线l与半径为1的⊙O相切于点A,弦BC∥l,D为圆上一点,∠ADB=30°,连接OB、OA,OA交BC于点E.(1)求∠AOB的度数;
(2)求BC的长.
考点:切线的性质
专题:
分析:(1)根据同弧所对的圆心角和圆周角的性质就可求得;
(2)根据切线的性质求得OA⊥直线l,然后根据BC∥l,求得OA⊥BC,最后通过解直角三角形从而求得BC的长.
(2)根据切线的性质求得OA⊥直线l,然后根据BC∥l,求得OA⊥BC,最后通过解直角三角形从而求得BC的长.
解答:解:(1)∵∠ADB=30°,
∴∠AOB=2∠ADB=2×30°=60°,;
(2)∵直线l与半径为1的⊙O相切于点A,
∴OA⊥直线l,
∵BC∥l,
∴OA⊥BC,
在RT△BOE中OB=1,
∴BE=OB×sin∠AOB=
,
∴BC=2BE=2×
=
.
∴∠AOB=2∠ADB=2×30°=60°,;
(2)∵直线l与半径为1的⊙O相切于点A,
∴OA⊥直线l,
∵BC∥l,
∴OA⊥BC,
在RT△BOE中OB=1,
∴BE=OB×sin∠AOB=
| ||
| 2 |
∴BC=2BE=2×
| ||
| 2 |
| 3 |
点评:本题考查了切线的性质,圆心角和圆周角的性质,解直角三角形等,熟练掌握性质和解直角三角形的方法是解题的关键.

练习册系列答案
相关题目
若α,β是方程x2-2x-3=0的两个实数根,则α+β的值是( )
| A、2 | B、-2 | C、3 | D、-3 |
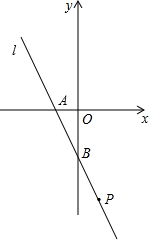 如图,已知,直线l分别交x轴y轴于A、B两点,OA、OB的长满足
如图,已知,直线l分别交x轴y轴于A、B两点,OA、OB的长满足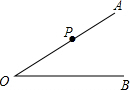 如图,已知∠AOB,P是射线OA上一点,按下列要求作图(保留作图痕迹,不要求写作法)
如图,已知∠AOB,P是射线OA上一点,按下列要求作图(保留作图痕迹,不要求写作法) 如图,已知点P在锐角∠AOB内部,∠AOB=α,在OB边上存在一点D,在OA边上存在一点C,能使PD+DC最小,此时∠PDC=
如图,已知点P在锐角∠AOB内部,∠AOB=α,在OB边上存在一点D,在OA边上存在一点C,能使PD+DC最小,此时∠PDC=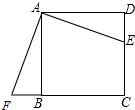 如图,在边长为6的正方形ABCD中,E是CD上一点,F在CB的延长线上,且DE=BF.
如图,在边长为6的正方形ABCD中,E是CD上一点,F在CB的延长线上,且DE=BF.