题目内容
13. 函数y=$\frac{1}{x}$和y=$\frac{4}{x}$在第一象限内的图象如图所示,点P是y=$\frac{4}{x}$的一个动点,CO⊥x轴于点C,PD⊥y轴于点D,PD、PC交y=$\frac{1}{x}$图象于点B,A.下列结论:
函数y=$\frac{1}{x}$和y=$\frac{4}{x}$在第一象限内的图象如图所示,点P是y=$\frac{4}{x}$的一个动点,CO⊥x轴于点C,PD⊥y轴于点D,PD、PC交y=$\frac{1}{x}$图象于点B,A.下列结论:①△ODB与△OAC面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=$\frac{1}{3}$PA.
其中正确的结论是( )
| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②④ |
分析 由于点P在y=$\frac{4}{x}$上,点A、B在y=$\frac{1}{x}$上,根据反比例函数系数k的几何意义,对各结论进行判断.
解答 解:由反比例函数系数k的几何意义判断各结论:
①△ODB与△OCA的面积相等;正确,由于A、B在同一反比例函数图象上,则两三角形面积相等,都为$\frac{1}{2}$.
②PA与PB始终相等;错误,不一定,只有当四边形OCPD为正方形时满足PA=PB.
③四边形PAOB的面积不会发生变化;正确,由于矩形OCPD、三角形ODB、三角形OCA为定值,则四边形PAOB的面积不会发生变化.
④∵S△OPA:S△OAC=$\frac{3}{2}$:$\frac{1}{2}$=3:1,
∴($\frac{1}{2}$PA•OC):($\frac{1}{2}$AC•OC)=3:1,
∴PA:AC=3,
∴CA=$\frac{1}{3}$PA;正确;
故一定正确的是①②④.
故选C.
点评 此题考查了反比例函数的几何意义、三角形的面积以及四边形的面积.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
4.将抛物线y=2(x-1)2-1,先向上平移2个单位,再向右平移1个单位后其顶点坐标是( )
| A. | (2,1) | B. | (1,2) | C. | (1,-1) | D. | (1,1) |
1.若正三角形的边长为2cm,则这个正三角形的面积是( )cm2.
| A. | 6 | B. | 4 | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
8.一元二次方程(x+2)(x-4)=0的两根为( )
| A. | x1=-2,x2=4 | B. | x1=-2,x2=-4 | C. | x1=2,x2=4 | D. | x1=2,x2=-4 |
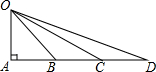 如图,在Rt△OAD中,∠A=90°,B,C在AD边上,且OA=AB=BC=CD,有下列结论:①△AOB∽△BOD:②△BOC∽△BDO:③△COD∽△BDO,其中成立的有②(选填序号)
如图,在Rt△OAD中,∠A=90°,B,C在AD边上,且OA=AB=BC=CD,有下列结论:①△AOB∽△BOD:②△BOC∽△BDO:③△COD∽△BDO,其中成立的有②(选填序号) A、B两地相距30千米,甲、乙二人同时从A地骑自行车去B地所走的路程y(千米)与时间x(时)之间的关系如图所示,下列说法①两人同时到达B地;②从出发1.5时以内,甲一直在乙的前面;③乙一直保持匀速前进;④在距离B地12千米处甲追上了乙,其中描述正确的是个数是( )
A、B两地相距30千米,甲、乙二人同时从A地骑自行车去B地所走的路程y(千米)与时间x(时)之间的关系如图所示,下列说法①两人同时到达B地;②从出发1.5时以内,甲一直在乙的前面;③乙一直保持匀速前进;④在距离B地12千米处甲追上了乙,其中描述正确的是个数是( )