Question

3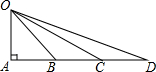．如图，在Rt△OAD中，∠A=90°，B，C在AD边上，且OA=AB=BC=CD，有下列结论：①△AOB∽△BOD：②△BOC∽△BDO：③△COD∽△BDO，其中成立的有②（选填序号）

Answer 1

分析 根据勾股定理得到OB=$\sqrt{2}$，OC=$\sqrt{5}$，OD=$\sqrt{10}$，求得$\frac{OC}{OD}=\frac{OB}{BD}$，由于∠OBD=∠DBO，根据相似三角形的判定定理即可得到结论．

解答 解：设OA=AB=BC=CD=1，
∵∠A=90°，OA=AB=BC=CD，
∴OB=$\sqrt{2}$，OC=$\sqrt{5}$，OD=$\sqrt{10}$，
∴$\frac{OC}{OD}=\frac{\sqrt{2}}{2}$，$\frac{OB}{BD}$=$\frac{\sqrt{2}}{2}$，
∴$\frac{OC}{OD}=\frac{OB}{BD}$，
∵∠OBD=∠DBO，
∴△BOC∽△BDO，
故答案为：②．

点评 本题考查了相似三角形的判定，勾股定理，熟练掌握相似三角形的判定定理是解题的关键．