题目内容
如图，要建一个苗圃，它的宽是a=4.8厘米，高b=3.6米．苗圃总长是10米．（1）求苗圃的占地面积；
（2）覆盖在顶上的塑料薄膜需要多少平方米？
考点：勾股定理的应用
专题：
分析：（1）利用图形得出占地面积为ad，进而得出答案；
（2）首先根据勾股定理求得直角三角形的斜边，即是矩形的宽．再根据矩形的面积公式计算即可．
（2）首先根据勾股定理求得直角三角形的斜边，即是矩形的宽．再根据矩形的面积公式计算即可．
解答：解：（1）苗圃的占地面积为：ad=4.8×10=48（m2）；
（2）根据勾股定理，得直角三角形的斜边为
=6（m），
由矩形的面积公式，得覆盖在顶上的塑料布为：6×10=60（m2）．
（2）根据勾股定理，得直角三角形的斜边为
| 4．82+3．62 |
由矩形的面积公式，得覆盖在顶上的塑料布为：6×10=60（m2）．
点评：此题主要考查了勾股定理的应用，熟练运用勾股定理计算以及由立体图形抽象出平面图形是解题关键．
练习册系列答案
相关题目
一次函数y=-x-1的图象与y轴的交点坐标为（ ）
| A、（-1，0） |
| B、（1，0） |
| C、（0，1） |
| D、（0，-1） |
如图所示，梯形ABCD中，AD∥BC，∠B=90°，AB=14cm，AD=18cm，BC=21cm，点P从点A开始沿AD边向点D以每秒1cm的速度移动，动点Q从点C开始沿CB边向点B以每秒2cm的速度移动，如果P、Q分别从A、C同时出发，设移动时间为t秒．
已知△ABC中，AB=17，BC=21，CA=10，求BC边上的高AD．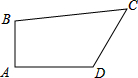
四边形ABCD，∠A=90°．AB=2，AD=2