题目内容
5.(1)若x+y=2,且(x+2)(y+2)=5,求x2+xy+y2的值;(2)已知x+y=4,xy=2,则x3y-x2y2+xy3的值.
分析 (1)先根据多项式乘多项式的法则把(x+2)(y+2)展开并代入数据求出xy的值,再根据完全平方公式把x+y=2两边平方,整理并代入数据即可求出x2+xy+y2的值;
(2)先提取公因式xy,再根据完全平方公式进行二次分解,然后代入数据计算即可得解.
解答 解:(1)∵(x+2)(y+2)=5,
∴xy+2(x+y)+4=5,
∵x+y=2,
∴xy=-3,
∴x2+xy+y2=(x+y)2-xy=22-(-3)=7.
(2)x3y-x2y2+xy3,
=xy(x2-xy+y2),
=xy[(x+y)2-3xy]
∵x+y=4,xy=2,
∴原式=2×[42-3×2]=2×10=20.
点评 本题考查了完全平方公式,运用整体代入思想,熟练对代数式进行变形是解题的关键.

练习册系列答案
相关题目
15.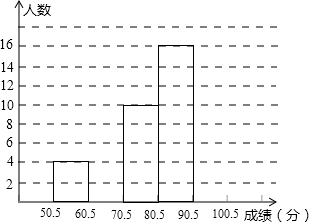 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)进行统计.请你根据尚未完成的频数分布表和频数分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)进行统计.请你根据尚未完成的频数分布表和频数分布直方图,解答下列问题:
(1)填充频数分布表的空格;
(2)补全频数直方图,并绘制频数分布折线图;
(3)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?
 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)进行统计.请你根据尚未完成的频数分布表和频数分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)进行统计.请你根据尚未完成的频数分布表和频数分布直方图,解答下列问题:| 分组 | 频数 | 频率 |
| 50.3-60.5 | 4 | 0.08 |
| 60.3-70.5 | 8 | 0.16 |
| 70.3-80.5 | 10 | 0.20 |
| 80.3-90.5 | 16 | 0.32 |
| 90.3-100.5 | 12 | 0.24 |
| 合计 | 50 | 1.00 |
(2)补全频数直方图,并绘制频数分布折线图;
(3)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?
13.若x<y,则下列式子正确的是( )
| A. | x-3>y-3 | B. | 3-x>3-y | C. | x+2>y+3 | D. | $\frac{x}{3}>\frac{y}{3}$ |
14.使$\frac{\sqrt{x-3}}{x-4}$有意义的x的取值范围是( )
| A. | x≥3 | B. | x≥3且x≠4 | C. | x≤3 | D. | x<3 |
15.下列各式成立的是( )
| A. | 4<$\sqrt{11}$<5 | B. | (x+1)(x+2)=x2+3x+2 | C. | 2-3=3-2 | D. | x3•x2=x3-x2 |
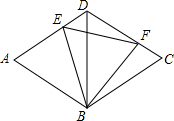 如图,菱形ABCD的较短对角线BD为5$\sqrt{3}$,∠ADB=60°,E、F分别在AD,
如图,菱形ABCD的较短对角线BD为5$\sqrt{3}$,∠ADB=60°,E、F分别在AD, 如图:∠B=60°,∠1=60°时,DE∥BC,理由是同位角相等,两直线平行.
如图:∠B=60°,∠1=60°时,DE∥BC,理由是同位角相等,两直线平行.